LA GEOMETRIA ELLITTICA – modello di Riemann

Questa geometria si ottiene sostituendo al quinto postulato di Euclide il seguente : “Ogni retta s passante per il punto P incontra sempre la retta prefissata r”

Questo postulato nega il quinto postulato in relazione all’esistenza della parallela ad una retta condotta per un punto.

Anch’essa sarà non contraddittoria ,ossia non porterà mai ad affermare un asserto e contemporaneamente ad affermare l’asserto opposto, se è possibile trovare un modello capace di soddisfare sia i primi 4 postulati euclidei sia questo nuovo elaborato da Riemann.

Come enti primitivi della geometria di Riemann consideriamo:

• il piano di Riemann costituito da qualunque superficie sferica (fig. 15)
• il punto di Riemann costituito da una qualunque coppia di punti diametralmente opposti alla superficie sferica (fig. 16)
• la retta di Riemann costituita da una qualsiasi circonferenza massima (fig. 6)

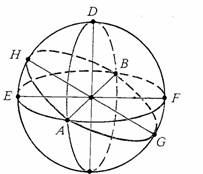
fig. 15 fig. 16

Ad esempio il postulato “Per due punti del piano passa una sola retta” è soddisfatto?

Sì,perché fissati due punti diametralmente opposti.

P’= (A,B) e P’’= (C,D)

è unica la retta di Riemann,ossia la circonferenza massima passante per essi. (fig. 17)

                                                   

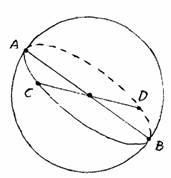
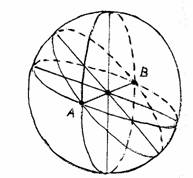
fig. 17 fig. 18

Ad esempio,il postulato “Per un punto del piano passano infinite rette” è soddisfatto?

Sì,perché fissato un punto di Riemann,ossia due punti diametralmente opposti,allora per esso passano infinite rette di Riemann,ossia infinite circonferenze massime. (fig. 18)

Il nuovo postulato è soddisfatto perché fissato un punto di Riemann e una retta di Riemann (ossia una coppia di punti diametralmente opposti e una circonferenza massima) allora ogni altra retta di Riemann passante per il punto di Riemann interseca sempre la circonferenza massima in due punti diametralmente opposti,ossia in un punto di Riemann. (fig. 19)

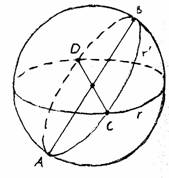 fig. 19

In conclusione non esiste alcuna retta di Riemann passante per un punto di Riemann e parallela a una prefissata retta di Riemann:questa nuova geometria è pertanto valida al pari della geometria euclidea.

Introduzione al problem solving nell’insegnamento della matematica. Il caso studio “Le dita del marziano”

Lavoro presentato da:

Pisano R., Ragone G., Rossi M., Russo A.

facenti parte del

Gruppo S.I.C.S.I, Indirizzo F.I.M., DM2, Università degli studi di Napoli Federico II

1. Introduzione alla tecnica del Problem Solving

L’attivita’ di problem posing¹ e di problem solving non devono essere identificate con quella di risoluzione di esercizi applicativi; esse sono attività più complesse. Gli esercizi applicativi possono essere risolti utilizzando concetti e regole già apprese, mentre la soluzione di un problema nuovo richiede capacità decisionali e l’utilizzazione di procedure e di strategie da scoprire. La strategia di risoluzione di un problema comporta l’esplorazione di regole (esperienze, procedure, leggi,...), l’analisi della situazione da più punti di vista, l’utilizzazione di regole anche nuove e la capacità di valutare la risolubilità del problema stesso.

Il problem solving potrebbe essere definito come un approccio didattico teso a sviluppare, sul piano psicologico, comportamentale ed operativo, l'abilità di soluzione di problemi. Generalmente il problem solving² è associato allo sviluppo delle abilità logico-matematiche di risoluzione di problemi. Tuttavia questi non si rivela l'unica area didattica che può giovarsi di dette abilità: problem solving, in un’ottica interdisciplinare, può dire uso corretto dell'abilità di classificazione di situazioni problematiche e capacità, quindi, di risolvere problemi-tipo analoghi, siano essi pertinenti all'area logico-matematica o meno (Web). Quindi, alla fine esso è un metodo di ricerca e di scoperta, che può comunemente essere applicato nelle diverse aree didattiche. Inoltre il metodo di soluzioni dei problemi, del quale il problem solving è una sfaccettatura, pone, come nucleo operativo, la scoperta ed il dominio di situazioni problematiche in generale, che possono sviluppare le potenzialità euristiche dell'allievo, e le sue abilità di valutazione e di giudizio obiettivo.

“ll problem solver strategico è come un esperto marinaio che, in mezzo all'oceano, cerca di prevedere e programmare le proprie azioni sulla base delle condizioni del mare in quel momento. Deve prevedere l'insorgere di imprevisti e prepararsi ad affrontarli confidando soltanto sulla sua "consapevolezza operativa", non sul controllo assoluto degli eventi. Non solo, ma egli non conosce e non può conoscere né la profonda verità del mare né tantomeno il perché dei suoi mutamenti. Eppure con questa sua conoscenza limitata al "come fare" attraversa gli oceani e fronteggia le tempeste adattando sempre il suo agire all'evolversi degli eventi”. (La terapia dell'azienda malata, 2000)

Il metodo della didattica per problemi consente agli allievi di apprendere a risolvere, con gradualità, problemi sempre più complessi che permettono allo studente di acquisire abilità cognitive di livello elevato. Un problema può essere una domanda che richiede una risposta precisa ed esauriente, oppure, un quesito che richiede l’individuazione o la costruzione di regole e di procedure che soddisfino condizioni predefinite e consentano di risolvere il quesito stesso.

Riteniamo che la didattica per problemi abbia una cruciale valenza educativa-formativa e consenta di far acquisire ad ogni allievo gli obiettivi didattici pre-fissati (a livello disciplinare o pluridisciplinare). L’attività di insegnamento-apprendimento per problemi deve consentire a ciascun allievo di: 

• Ricercare dati ed informazioni;
• Fare stime e calcoli ...;
• Formulare ipotesi risolutive;
• Proporre soluzioni;
• Prendere decisioni.

La didattica per problemi deve essere intenzionale e funzionale rispetto agli obiettivi educativi e didattici da conseguire, in termini di conoscenze, competenze e capacità. Durante la soluzione di un problema l’allievo deve essere messo (dal docente) in condizione di scoprire (e ri-scoprire) ed acquisire, autonomamente, conoscenze nuove. E’importante sottolineare che, in questo tipo di didattica, devono essere rispettate alcune regole fondamentali di relazione:

• I problemi non devono essere imposti, in modo direttivo, ma essere discussi e condivisi dal gruppo classe e/o nei piccoli gruppi;
• I docenti assumono la funzione di guida metodologica, di assistenza e di consulenza per ciascun allievo o per il gruppo di alunni impegnato nella soluzione del problema.
• Il docente svolge le funzioni di tutor;

Inoltre la didattica per problemi consente il conseguimento dei seguenti obiettivi per ciascun allievo:

a) Apprendere ad organizzare in modo significativo le proprie conoscenze;

b) Apprendere a valutare l’utilità delle conoscenze acquisite, rispetto agli obiettivi prefissati in termini di conoscenze, competenze e capacità;

c) Sviluppare l’attitudine ad affrontare problemi nuovi ed imprevisti e a trasferire le conoscenze acquisite in contesti diversi (transfer);

d) Decidere in condizioni d’incertezza oltre che di certezza;

e) Sviluppare la capacità di dominare situazioni anche complesse;

f) Apprendere ad utilizzare appropriati metodi di comunicazione oltre che di documentazione;

g) Apprendere ad apprendere.

Quando un allievo s’imbatte in un problema, inizialmente ne sa molto poco, ma potrà diventare esperto di quel particolare problema, formulando ipotesi risolutive, seppure inadeguate ed insoddisfacenti, criticando, rivedendo ed affinando le ipotesi stesse, dopo averle messe alla prova.

Comprendere un problema, quindi, significa capirne le difficoltà, tentare di risolverlo con un’applicazione tenace e responsabile, con perseveranza e gratificazione intellettiva, legata alla soluzione del problema stesso. Con tale metodo si possono sviluppare alcuni aspetti fondamentali della personalità quali:

1) La responsabilità,

2) L’autonomia,

3) La fiducia in sé,

4) La stima di sé,

5) La cooperazione con gli altri, 

6) La solidarietà,

7) Le capacità decisionali.

L’attività didattica deve essere progettata e programmata collegialmente facendo in modo che gli allievi risolvano i problemi in piccoli gruppi, costituiti ad es. da cinque studenti. I problemi possono essere scomposti in sottoproblemi, più semplici da risolvere. I gruppi scelgono un loro referente che illustra ai componenti degli altri gruppi le procedure che hanno consentito la soluzione del problema. In tale fase, la funzione del docente consiste nell’insegnare agli allievi del gruppo classe a trovare la soluzione o le soluzioni (anche quelle non ottimizzate) del problema. Generalmente un problema ne genera un altro: la soluzione di un problema può essere, infatti, il presupposto per la posizione di un altro. Il filosofo ed epistemologo K. Popper sostiene che

“[…] la ricerca scientifica consiste nel risolvere problemi”, […] la vita è costituita da problemi da risolvere” e, quindi, che“ apprendere a risolvere problemi significa apprendere a vivere […]’’  (Popper K.).

1L’attività di problem posing consiste nel concettualizzare un problema, mediante una riflessione sulla situazione problematica nella quale l’allievo s’imbatte.

2 Ad onore del vero, oltre ai testi citati in bibliografia, abbiamo consultato, sebbene non specificatamente citati, molti siti Web che trattavano in maniera più o meno esaustiva gli argomenti di cui sopra. Il loro non totale riporto in bibliografia, e di questo ci scusiamo con il lettore, è dovuto alla mancanza, in molti casi, di una sistematizzazione bibliografia dei contenuti esposti dai siti stessi. Pertanto, con la sigla Web, indicheremo il riferimento bibliografico consultato in rete diversi da quelli suggeriti dal Prof. Tortora.

 2. Cenni sul problem solving di tipo metacognitivo

Recenti studi (Web) sono proiettati all’applicazioni di risoluzioni di problemi mediante un approccio definito come problem solving di tipo metacognitivo; esso tende ad essere, rispetto al metodo classico di cui sopra, un'espansione applicativa.

La routine del problem solving prevede diversi momenti, durante i quali possono essere sviluppati diversi processi di controllo propri delle abilità metacognitive.

Di seguito, sintetizziamo le principali relazioni che sussistono tra la tecnica del problem solving e le attività metacognitive che accompagnano l’uso di tale tecnica.

  Il problem solving metacognitivo diviene quindi un palestra per l'abilità di autoregolazione poiché, in modo sempre più puntuale, i ragazzi saranno in grado di monitorare i processi e di valutare i gradi di utilità, necessità ed appropriatezza dei diversi processi risolutivi, nonché di classificare le rappresentazioni personali di procedure, ed attiveranno positivi transfer degli apprendimenti (Varriale).  

 

Tab. 1 relazione tra il problem solving e le attività metacognitive di controllo

PROBLEM SOLVING	ATTIVITA' METACOGNITIVE DI CONTROLLO
Comprensione	Prima di lavorare rifletti: Quello che vai ad affrontare è proprio un problema? Cosa sai su come si fa? Hai incontrato problemi simili?
Previsione	Prima di lavorare prevedi: Cosa ti può aiutare? Quanto tempo hai? Di quali/quanti strumenti hai bisogno? Qual è l'ambiente in cui svolgerai il compito?
Pianificazione	Organizzati: Identifica il problema. Vuoi/puoi lavorare da solo o in gruppo? Reperisci materiali e strumenti. Scegli i metodi di rappresentazione dei dati. Stabilisci i tempi di lavoro.
Monitoraggio	Mentre svolgi il compito risolutivo controlla: Sei sulla strada giusta? Cosa va eliminato o invece salvato? Il compito ti sembra facile o difficile? Se non riesci ad andare avanti, cosa fai? Quella che hai trovato e' LA soluzione?
Valutazione	Quando hai risolto il problema, guarda indietro: Le tue previsioni e la tua pianificazione ti sono stati utili? Hai lavorato bene? Si sarebbe potuto fare in un altro modo? Questa procedura di risoluzione può esserti utile in altri compiti? C'è stato qualche problema insuperabile?

2. Il metodo della didattica per problemi si fonda sulla motivazione ad apprendere.

L’intuizione intesa come conoscenza diretta ed immediata della realtà, di un fenomeno, di una situazione, può giocare un ruolo importante nella soluzione di un problema. Le difficoltà, per l’alunno, possono presentarsi in una delle seguenti fasi:

a) Lettura del problema,

b) Comprensione del problema,

c) Applicazione di procedure risolutive,

d) Codifica della risposta.

Le fasi di risoluzione di un problema, invece, possono essere le seguenti:

1) Presentazione del problema,

2) Riflessione sul problema,

3) Soluzione del problema,

4) Discussione in gruppo (brain storming).

Nella soluzione di problemi intervengono anche processi metacognitivi quali:

a) l’analisi delle proprie conoscenze,

b) la loro utilizzazione pratica.

Durante la tecnica del PS può essere adottato il metodo del brain storming. Esso può essere utilizzato dal docente per animare i lavori di gruppo, soprattutto nella fase in cui si discute la soluzione di un problema. Per semplificare la risoluzione di un problema si ricorre ad una sua modellizzazione ossia ad una sua rappresentazione euristica, che ne riproduce le caratteristiche essenziali. Il modello interviene in due fasi relative alla soluzione di un problema:

• Quando dal modello si passa a ciò che il solutore deve fare per risolvere il problema,
• Quando dalla situazione problematica reale si arriva alla costruzione di un modello risolutivo.

Il modello preliminare alla soluzione di un problema può essere un modello già strutturato, oppure un modello formato solo in parte e, quindi, in via di formazione completa. Il modello può essere adeguato per risolvere il problema oppure non è adeguato del tutto o solo in parte, per giungere alla soluzione del problema. Esiste una varietà di modelli, articolati in fasi, per il problem solving. Secondo alcuni studiosi (Web) per il modello tipo classico si possono articolare quattro fasi:

• Fase iniziale: il solutore tenta di comprendere di che cosa tratta il problema che ha di fronte e che cosa deve fare;
• Fase di attacco: il solutore saggia una prima ipotesi di soluzione, che può condurlo in porto o no; in quest’ultimo caso deve riformulare le ipotesi;
• Fase di controllo: il solutore confronta la propria soluzione con lo stimolo posto dal problema, per valutarne l’efficacia;
• Fase di estensione: la soluzione di un problema dovrebbe portare alla formulazione di un altro problema.

Inoltre in tale modello l’attività di problem solving è influenzata da condizioni esterne e da condizioni interne. Le condizioni esterne sono costituite da:

a) Stimoli verbali e non,

b) Indicazioni, direttive finalizzate a favorire la concettualizzazione del problema,

c) Istruzioni che hanno la funzione di agevolare la soluzione del problema.

Le condizioni interne sono legate alle differenze individuali e dipendono dalla:

• Quantità di informazioni immagazzinate,
• Facilità di richiamare alla memoria le informazioni stesse,
• Capacità di selezionare i concetti,
• Flessibilità nel formulare ipotesi,
• Capacità di saper confrontare il caso specifico con il caso generale.

3. Modellizzazione della tecnica del Probem solving

Contributi al problem solving vengono dalle teorie psicologiche come la gestalt, il comportamentismo, il cognitivismo (Polmonari, 245-261) e dalle scienze dell’informazione (metodo top down e bottom up (Booch; Cantor; Pisano R.). A questo punto per una rapida e globale visione dell’approccio metacoglitivo riportiamo i seguenti digramma B. e C. che specificano solo passi operativi (tralasciando quelli cognitivi).

4. Il problem solving nell’insegnamento della matematica. Piccola sintesi dell’interpretazione di Poyla

L’attività’ di problem solving ha una sua specifica applicazione in matematica. Secondo il matematico George Polya (Poyla) la risoluzione di un problema si sviluppa in quattro fasi:

Ÿ Comprendere il problema,

Ÿ Ideare un piano per trovare la soluzione,

§ Eseguire il piano,

§ Verificare e valutare il procedimento e controllare il risultato.

Si possono distinguere tre aspetti relativi alla strategia di risoluzione dei problemi:

a) Come si presenta il problema,

b) Come interagiscono le caratteristiche del contesto problematico con le conoscenze ed i modelli di ciascun solutore,

c) Come sono analizzati i problemi e come il solutore stesso analizza la propria struttura o matrice cognitiva.

Risolvere un problema matematico implica la trasformazione della struttura conoscitiva del solutore da uno stato iniziale “i” ad uno stato finale “f”, come avviene per il processo d’apprendimento in generale. Nell’attività’ di problem solving il docente valuta:

1. Il tempo impiegato nella soluzione del problema,

2. La precisione, in altre parole, la qualità e la quantità di errori commessi (analisi dell’errore).

Nell’attività di risoluzione di problemi l’allievo deve acquisire le seguenti competenze intese come esiti in uscita:

• Comprendere il testo di un problema,
• Individuare i dati essenziali, 
• Individuare quelli mancanti,
• Individuare relazioni e corrispondenze,
• Costruire relazioni e corrispondenze,
• Utilizzare in modo consapevole tecniche e procedure di calcolo,
• Sviluppare algoritmi risolutivi,
• Controllare la validità degli algoritmi risolutivi individuati o costruiti,
• Matematizzare il problema da risolvere, attraverso processi di generalizzazione e di simbolizzazione, questa operazione riduce l’effetto della complessità,
• Padroneggiare modelli risolutivi in condizioni di certezza e in condizioni d’incertezza,
• Utilizzare gli strumenti informatici a disposizione,
• Allenarsi al rigore e alla precisione mentale,
• Comprendere e utilizzare i codici formali.

In particolare: in merito alla concettualizzazione di un problema matematico (mathematical problem posing) può essere utile servirsi delle tabelle seguenti:
 

Dato il testo di un problema	Individuare i dati utili alla sua risoluzione.
Dato il testo di un problema	Individuare gli eventuali dati che lo rendono ambiguo
Data una situazione problematica	Individuare il problema che la rappresenta e gli elementi utili per la sua risoluzione.
Dato un enunciato	Individuare ipotesi, conclusioni e l’ambito di applicabilità del problema.

Relazioni tra dati:

Dato il testo di un problema	Organizzare i dati in una tabella
Dato il testo di un problema	Organizzare i dati in un diagramma
Data una situazione problematica	Organizzare le relazioni dirette e inverse tra i dati
Dato un enunciato	Organizzare relazioni astratte di tipo simbolico tra dati.

Metodi risolutivi. Determinare un algoritmo che permetta d’individuare un risultato controllandone i limiti di validità o di pertinenza:

 

Dato il testo di un problema	Risolvere il problema con un metodo intuitivo
“	Risolvere il problema per analogia.
Data una situazione problematica	Risolvere il problema con il metodo delle approssimazioni successive.
Dato l’enunciato di un problema	Risolvere il problema con metodi grafici (compreso il metodo geometrico.
“	Risolvere il problema con metodi algebrici
“	Risolvere il problema con metodi informatici
“	Risolvere il problema con metodi misti.

5. Applicazione del problem solving. Il caso studio dell’ “le dita del marziano”.

Supponiamo di riuscire un giorno a contattare un marziano proponendogli di risolvere una semplice equazione:

x² - 16 x + 41 = 0

Se lui ci dicesse che la differenza delle radici vale 10, quante dita avrebbe il marziano?

La finalità didattica che si vuole raggiungere con un problema di questo tipo è la comprensione dell’importanza dei sistemi di numerazione e del cambiamento di base. Non è tutto! Risolvere problemi del genere interessa anche un’altra sfera matematica, l’algebra, ed in particolare la scomposizione di trinomi di secondo grado nonché la risoluzione di equazioni di secondo grado e sistemi di equazioni di primo grado a due incognite. Sarà compito dell’insegnante indirizzare gli allievi verso la soluzione più consona agli obiettivi didattici prescelti. Precisiamo che tale attività didattica si pone come verifica di apprendimento delle nozioni di cui sopra¹.

Un primo ingenuo approccio a questo problema è risolvere l’equazione data con la formula risolutiva nota per cercare le due radici x₁ ed x₂ e verificare che la loro differenza è 10.

Facendo in questo modo ci si accorge in breve tempo che “i conti non tornano”… le due radici non sono numeri interi e la loro differenza non è 10!

• Come risolvere allora il problema?
• Qual è il nesso che lega le soluzioni dell’equazione data con le dita del marziano?

Questo è il suggerimento che daremmo alla scolaresca per instradarli verso la risoluzione del problema.

: A questo punto daremmo libero sfogo all’intuizione dei ragazzi limitandoci esclusivamente a fare da mediatori instradandoli verso la soluzione più congeniale agli insegnamenti che desideriamo trasmettere agli alunni. Volendo richiamare i concetti di risoluzione e scomposizione di equazioni di secondo grado, sistemi di numerazione, cambiamento di base e risoluzione di sistemi di equazioni di primo grado a due incognite, la soluzione da noi proposta è la seguente:

SOLUZIONE 1.

La chiave sta nel capire che il numero di dita del marziano corrisponde alla base del suo sistema di numerazione. Si tratta, quindi, di individuare qual è la base B, esprimendo con la quale i numeri, si riesce a soddisfare la condizione dettata dal problema. Innanzitutto possiamo dire che si tratta di una base maggiore di 6 visto che la cifra 6 compare nell'equazione.

Facciamo prima un piccolissimo richiamo sulle equazioni di 2° grado. Supponendo che le radici di un’equazione siano a e b e che il coefficiente di x² sia unitario, l’equazione può essere riscritta in questo modo:

(x - a) (x - b)=0

cioè:

x² - (a + b) x + a b = 0

ossia si ha che il coefficiente di x è uguale alla somma delle radici cambiata di segno e il termine noto è il prodotto delle due radici. A questo punto, visto che conosciamo i coefficienti dell'equazione, possiamo scrivere (denotando con B la base di numerazione del marziano espressa in base 10 e supponendo a>b ):

(*)

Sommando membro a membro le equazioni I e III si ottiene:

2a = (2B + 6)₁₀

da cui:

a = (B + 3)₁₀

Pertanto dalla equazione III si ha:

b = a - (B)₁₀ = (B + 3)₁₀ - (B)₁₀ = (3)₁₀

Infine dalla II si ricava:

[3 (B + 3)]₁₀ = [4 B + 1]₁₀ 

3B + 9 = 4B +1 

B = 8

Essendo la base di numerazione del marziano pari al numero di dita, si conclude che il marziano ha 8 dita.

OSSERVAZIONE

Le soluzioni a, b e B del sistema (*) sono state trovate utilizzando il metodo di addizione e sottrazione. Qualora l’insegnante lo ritenesse necessario, si potrebbero utilizzare anche altri metodi risolutivi.

Possiamo verificare che riscrivendo tutto in base 10 si ha:

x² - 14 x + 33 = 0

le cui radici sono x₁=3 e x₂=11.

Facendo la differenza si ottiene:

x₁ - x₂ = 11-3 =8

risultato accettabile in quanto (8)₁₀ = (10)₈.

Se invece volessimo focalizzare l’attenzione solo sulla scomposizione di un trinomio di secondo grado con somma e prodotto e sul cambiamento di base di numerazione, si potrebbe indirizzare gli allievi verso la seguente strategia di ragionamento:

SOLUZIONE 2.

L'equazione di secondo grado in questione è di quelle che, se si cercano soluzioni intere, si possono leggere anche così: trovare 2 numeri tali che la loro somma sia uguale al coefficiente del termine di primo grado (16) e il loro prodotto al termine noto (41).

Partiamo dal prodotto. 41 è primo, dunque è dato da 1 * 41. La differenza è 40 e deve essere 10.

Cambiamo base e proviamo a scendere.

In base 9 il prodotto è 37, anch'esso primo. Nulla da fare.

Scendiamo ancora.

In base 8 il prodotto è 33, che è dato anche da 3 * 11.

Si controllano a questo punto la somma che è 14 (16 in base 8) e la differenza che è 8 (10 scritto in base 8).

Possiamo dunque che la base del sistema di numerazione e quindi le dita del marziano sono 8.

OSSERVAZIONE

Va osservato che un tale approccio oltre a non essere rigoroso, ha il difetto di essere poco perseguibile qualora la base di numerazione fosse maggiore di 10. L’ultima soluzione proposta si differenzia dalle due precedenti per ciò che concerne la risoluzione dell’equazione di secondo grado data dal problema. In questo tipo di approccio, infatti, si è fatto uso delle formule risolutive classiche.

SOLUZIONE 3.

Per il marziano la differenza delle due radici dell’equazione

x² - 16 x + 41 = 0

risulta essere 10 (ovviamente nel suo sistema di numerazione o base) ; questo vuol dire che:

sostituendo si ottiene:

ovviamente questa equazione è soddisfatta solo in una base m (che corrisponde al numero di dita del marziano) che trasformata in base 10 diventa:

in conclusione, l’equazione risulta soddisfatta se e solo se la base nella quale è stata scritta è 8. Infatti

Base 8	Base 10
16	14
41	33
10	8

6. Conclusioni e riflessioni

È noto che la scuola costituisce un ambito importante di socializzazione, un ambito nel quale si apprendono e perfezionano competenze culturali e sociali.

È indubbio che parlando di scuola si debba prendere in considerazione, fra gli altri aspetti, anche la qualità sociale dell'educazione, elemento da cui può dipendere in varia misura l'insuccesso scolastico.

Il tema del "buon insegnante" o anche dell'insegnante "ideale" è stato ampiamente studiato in psicologia dell'educazione, soprattutto in rapporto alla fascia adolescenziale, poiché è proprio l'allievo adolescente, quello che da un lato, mostra le aspettative più precise ed articolate nei confronti dei propri insegnanti, dall'altro, è anche l'allievo tendenzialmente più difficile poiché più incline a demotivazione scolastica, più capace di abbassare la credibilità dell'insegnante attraverso propri comportamenti.

Gli insegnanti giocano un ruolo importante nel rendimento scolastico. Questo fatto è piuttosto comprensibile: se l'insegnante si centra di preferenza sugli individui rischia di perdere il controllo del gruppo. Questa è la situazione in cui facilmente incorrono gli insegnanti meno esperti, che mostrano difficoltà ad interagire per tempi prolungati con la classe intera. D'altra parte, saper interagire produttivamente con un gruppo di adolescenti prevede che siano attivati i loro livelli di partecipazione e di motivazione.

Insomma, producono risultati migliori in termini di riuscita scolastica quelle scuole in cui è incoraggiata la partecipazione attiva degli allievi, in cui è messo in pratica l'ascolto reciproco fra insegnanti ed alunni, in cui gli insegnanti possono effettivamente programmare collegialmente le attività e contare sulla supervisione di insegnanti esperti (più anziani).

In conclusione riteniamo che acquisire, progressivamente, capacità di problem posing e di problem solving serve ad agevolare le potenzialità d’apprendimento di un allievo, che manifesterà desiderio di coinvolgimento nelle attività di formazione, all’interno dell’organizzazione. Tutte le discipline sono potenzialmente portatrici e generatrici di problemi, la matematica in particolare è una disciplina costituita da procedure o algoritmi basati sulle capacità di analisi, di sintesi e di capacità di concettualizzare e risolvere problemi.

Appendice

I compiti di sviluppo

Il successo e l’insuccesso scolastico si collocano entro una matrice interattiva che contestualizza il percorso scolastico dello studente attraverso la descrizione delle dinamiche e dei processi socio-psicologici che si verificano in classe, nonché attraverso la comprensione di rappresentazioni, valori e significati condivisi dagli insegnanti e dagli studenti che interagiscono all’interno dello stesso spazio. La natura sociale della conoscenza è considerata come il risultato delle interazioni di gruppi di persone che costruiscono insieme modi comuni di esprimersi usando linguaggi appropriati, di mettere a punto procedure e metodi più efficaci per raggiungere gli obiettivi comuni.

Le relazioni fra insegnanti e studenti sono caratterizzate da un processo basato sulla possibilità degli insegnanti di interagire con gli allievi sulla base delle rappresentazioni sociali più diffuse a livello di senso comune, riguardo quello che caratterizza uno studente di successo o di insuccesso.

Secondo alcuni studi, sono definiti i compiti di sviluppo, il lavoro che l’adolescente compie per superare ostacoli socio-culturali connessi al passaggio fra cicli di studio e la scelta del ciclo scolastico successivo all’istruzione obbligatoria. Entrambi questi passaggi possono indurre nell’adolescente (ad es.) situazioni di stress e ansia: sia per l’inserimento nella scuola superiore o nei centri di formazione professionali, sia per coloro che lasciano la scuola per accedere al mondo del lavoro. La situazione disagiata che l’adolescente vive costituisce l’occasione per verificare le proprie capacità. In più tali situazioni, non solo devono essere oggetto di oculato studio da parte del docente (attento), ma occorre che essi siano il punto di partenza per una didattica per problemi. Il superamento positivo di tale fase genera (o incrementa) la fiducia di se stessi di essere in grado di affrontare ulteriori compiti; quindi scatena un processo molto positivo di autostima. Al contrario, il non superamento del compito produrrà inevitabilmente la perdita di fiducia nelle proprie capacità di far fronte a situazioni e problematiche in modo soddisfacente. Allora, qual è il ruolo dell’insegnante in questo caso?

Perché l’alunno “va male” a scuola?

Gli adolescenti che affrontano i diversi compiti di sviluppo sono oggetto di valutazione da parte degli adulti: insegnanti e genitori; e di confronto con gli altri coetanei. Questo è un aspetto molto delicato nella crescita dell’adolescente. Infatti, il riconoscimento che gli è fornito ed impegnato nel superamento di un compito di sviluppo, incide notevolmente sul processo di costruzione della identità del ragazzo/a. Da qui, l’adolescente tenderà a costruire un’immagine positiva (o negativa) di se stesso. Solo quando ogni individuo percepisce di possedere qualità socialmente valorizzate in grado di relazionarsi bene con gli altri, si può convincere di poter interagire costruttivamente con l’ambiente sociale in cui vive.

Questo processo è talvolta (positivamente o negativamente) accompagnato da una interazione prolungata con i genitori o gli insegnanti. Oggetto della valutazione è qui il tipo di rapporti esistenti tra gli alunni e tra alunni ed insegnante, e cioè il genere di relazioni che permettono di creare in classe un clima favorevole all'acquisizione del sapere.

La prospettiva causalistica che ha dominato e che spesso domina tuttora all’interno dell’istituzione scolastica ha costruito un sistema di rappresentazioni che ha consentito di giustificare la presenza dello studente “diverso” (deviante, in condizioni di handicap o solamente l’alunno che “va male a scuola”) quale risultato delle differenze individuali tra gli alunni (differenze nell’intelligenza, nelle attitudini, negli interessi, nelle predisposizioni, nelle motivazioni, nel contesto socio-economico di provenienza) e legittimare quindi gli eventuali provvedimenti messi in atto dall’istituzione stessa per mano degli insegnanti. In questo modo l’intero sistema e gli stessi insegnanti sono stati deresponsabilizzati dal prendere criticamente in esame il proprio agire quotidiano. Ma la diversità, la devianza del ragazzo, non è solo una proprietà dell'azione compiuta dal ragazzo o una caratteristica della sua personalità o del suo carattere, come più frequentemente è chiamato in causa, ma è anche una conseguenza del fatto che l'insegnante applica delle regole di valutazione dettategli dal criterio di normalità/anormalità che il suo personale consenso all'istituzione gli impone. E questo, secondo me, è errato!

Il tema della comunicazione in classe si affronta partendo dall'osservazione diretta del comportamento comunicativo dell'insegnante, caratterizzato dal porre domande o dal fornire risposte, dal lodare, dal criticare o dall'ignorare dal trasmettere informazioni o dal riferire opinioni. L'intento sembra essere quello di valutare la capacità professionale dell'adulto tramite la qualità delle interazioni instaurate con gli alunni, tentando in alcuni casi di stabilire dei nessi tra lo stile comunicativo dell'insegnante e il rendimento degli allievi.

L'adolescente è impegnato, proprio negli anni della scuola superiore, in una complessa e lunga operazione di passaggio da un'identità appartenente al mondo infantile ad un'identità adulta e sociale. Questo processo implica per lui la necessità di separarsi da oggetti, affetti e comportamenti infantili, e passare ad acquisire autonomia delle proprie capacità e delle proprie relazioni sociali.

La scuola, senza dubbio, si inserisce in questa vicenda di trasformazione e passaggio. In effetti, essa rappresenta un campo di esperienza particolarmente significativo proprio in rapporto a quei processi in cui occorre dare prova di sé, misurarsi con le difficoltà, esporsi al giudizio, produrre risultati valutabili, ottenere una valutazione da un adulto competente ed autorevole. Insomma, per l'allievo, la scuola è, in primo luogo, la sede dove cresce il bisogno di sperimentarsi, di realizzare e produrre qualcosa in cui riconoscersi, qualcosa che possa essere valutato dagli altri e possibilmente approvato e apprezzato all'esterno per rimandare un'immagine concreta e ricca di sé.

Per comporre il quadro della relazione tra adolescenti e scuola occorre anche riflettere sul senso dell'apprendimento scolastico, in particolare sui significati concreti connessi alla funzione dell'imparare. In alcuni testi, si legge che imparare con successo significa crescere, affermarsi, vincere, controllare: l'imparare è una funzione importante e desiderabile perché sinonimo di passaggio a stadi più evoluti. Ma, l'adolescenza è dominata anche da oscillazioni e contraddizioni tra la voglia di crescere e la paura di uscire dall'infanzia. Pertanto, imparare potrebbe voler dire anche uscire dal gioco, dall'irresponsabilità e dalla dipendenza da chi sa di più. Dunque, il processo dell'imparare implica anche esperienze di incertezza, confusione e incomprensione, ed espone naturalmente a rischi di fallimento, di frustrazione e di fatica. Per i ragazzi è spesso cosa difficile e fonte di ansia tollerare lo stato di non conoscenza, la sensazione di non comprensione e controllo del nuovo da acquisire. L'apprendimento insomma, può essere per l'adolescente un'esperienza che ripropone e condensa le emozioni, i conflitti, e le ansie più intense.

Tuttavia, il rapporto tra le richieste della scuola e la realtà della condizione adolescente è certamente complesso e contraddittorio: se da un lato i caratteri del pensiero, della libertà dell'astrazione, e a formulare ipotesi, sembrano la migliore premessa per un forte impegno intellettuale, d'altro canto, l'investimento massiccio sulla propria realtà emotiva pongono, all’allievo, un ostacolo sulla possibilità di una convergenza tra compiti scolastici e compiti di sviluppo. Probabilmente la condizione necessaria perché tale convergenza si verifichi fattivamente è che l'adolescente possa sentire la scuola come un'occasione di sperimentazione positiva di sé, sede di riconoscimento e conferma di elementi necessari alla graduale conquista di nuove identità; ma sicuramente la condizione appena suggerita segue da una modifica (quasi) radicale del mondo-scuola.

In definitiva, nella scuola, occorrerebbe almeno recuperare i seguenti elementi:

• La motivazione allo studio
• Il significato dello studio
• Il significato della funzione educativa

Recuperare la motivazione

Occorrerebbe far percepire la scuola come spazio esperienziale che contiene opportunità di prova di sé, di affermazione, di scoperta, di evoluzione, di identificazione, di confronto, di gioco di idee, delle opinioni e di responsabilità. Infine, occorrerebbe ri-centrare l'immagine e la realtà della scuola sugli studenti, e non solo su talvolta impraticabili ed incomprensibili programmi e sull'istituzione, in modo che lo studente senta di essere il protagonista e percepisca le opportunità che la scuola offre come risposta ad un'esigenza formativa propria e non solo dettata da esterne burocrazie e pericolose politiche valide solo per fini istituzionali.

Recuperare il significato dello studio

Recenti studi sicsiini ci hanno portato alle seguenti riflessioni. Occorrerebbe, fondare la didattica nel suo complesso, non più come trasmissione di saperi, ma come ricostruzione di significati. Un sapere che sia sempre accompagnato da idee, motivi ed opinioni; proposte di contenuti che prevedano anche i modi di pensare e di valutare quei contenuti, percorsi di ragionamento che partano delle precedenti conoscenze di vissuto dei ragazzi.

Il significato della funzione educativa

Dobbiamo uscire da ciò che è rigidamente curricolare e mettere (quando è possibile) da parte l'iter scolastico per favorire "contenuti di relazione". Recuperare la relazione, in realtà, significa mettersi in gioco con tutto il proprio carisma e tutta la propria autorevolezza di ruolo come punto di riferimento adulto e colto, e come possibile modello di rapporto con il sapere e la conoscenza. Significa entrare in una relazione produttiva con gli studenti per condividere progetti, comunicare aspettative e restituire valori.

Bibliografia generale

• Booch G.: Object Solution, CA, Addison-Wesley (ed.), 1996
• Booch G.: Object-Oriented Analysis and Design with Applications, 2^nd edition, CA, Addison-Wesley (ed.), 1994
• Cantor M. R.: Object-Oriented Project Managment with UML, J. Wiley & Sons (eds.), New York, 1998
• Corbi E: Lucidi del corso, TP, S.I.C.S.I, a.a. 2001-02
• D’Amore B.: Problemi. Pedagogia e psicologia della matematica nell’attività di problem solving – Franco Angeli,
• Gardner M.: Enigmi e giochi matematici, Sansoni, Firenze (1959/1976), e poi BUR, Milano , (2001).
• Kline M.: Mathematical Thought from ancient to modern times, Oxford Univesity (ed.), New York, 1972, pp. 205-210; Trad. ital.: Storia del pensiero matematico, Vol. I, Einaudi editore, Torino, pp. 241-252
• Kolmogorov A.N, Aleksandorv A.D., Lavrent’ev M.A.: Le matematiche, Boringhieri editore, 1974, pp. 1-14
• Manara F. C. e Lucchini G.: Momenti del pensiero matematico, Mursia Editore, Milano, 1976, pp. 13-20, pp. 56-58
• Meschkowski H.: Mutamenti nel pensiero matematico, Boringhieri editori, 1973
• Milano, 1993.
• Polya G.: Come risolvere i problemi di matematica. Logica ed euristica – Feltrinelli, Milano.
• Polya G.: La Scoperta matematica. Capire, imparare e insegnare a risolvere i problemi, Feltrinelli, Milano.
• Popper K.: Logica della scoperta scientifica, Einaudi editore, 1970, pp. 5-31
• Russell B.: I principi della matematica, Newton & Compton editori, 1989, pp. 353-397
• Sarracino, Corbi E: Storia della scuola e delle istituzioni educative (1830-1999), Napoli, Liguori (Ed.), 2001, pp. 29-41, pp. 53-74
• Sawyer.: Guida all’insegnamento della Matematica, Boringhieri, Milano.
• Scurati C., Veronesi G.: Psicologia e Pedagogia, Edizioni Claire, Milano, 1984, pp. 129-195
• Smullyan R.: Qual è il titolo di questo libro. L’enigma di Dracula ed altri indovinelli, Zanichelli, Bologna, 1981.
• Web: “vari siti Web”

Siti consultati

• http://www.liceo-vallisneri.lu.it
• http://www.dm.unito.it/paginepersonali/arzarello
• http://www.stat.unipg.it/CIRDIS/Matematica2001/
• http://www.dm.unibo.it/umi
• imo.math.ca (IMO – International Mathematical Olympiad)
• http://olimpiadi.ing.unipi.it
• http://matematica.uni-bocconi.it
• http://utenti.tripod.it/math/

1Effettuando una previsione di tipo qualitativo (10 persone intervistate) è emerso che più del 50% ha risposto “non lo so”, esprimendo la loro convinzione che non sussiste alcun nesso logico (apparente) tra le dita della mano di un marziano e la soluzione matematica di una equazione di secondo grado.