Mouse in inglese significa topo... :)

Il mouse del computer viene tradotto in diverse lingue, 'souris' in francese, 'raton' in spagnolo, 'maus' in tedesco. In italiano il mouse è rimasto mouse. Non lo sapevano gli americani della IBM quando hanno tradotto un manuale d'istruzioni.
"Le palle dei topi sono da oggi disponibili come parti di ricambio. Se il vostro topo ha difficoltà a funzionare correttamente, o funziona a scatti, è possibile che esso abbia bisogno di una palla di ricambio. A causa della delicata natura della procedura di sostituzione delle palle, è sempre consigliabile che essa sia eseguita da un personale esperto. Prima di procedere, determinare di che tipo di palle ha bisogno il vostro topo. Per fare ciò basta esaminare la sua parte inferiore. Le palle dei topi americani sono normalmente più grandi e più dure di quelle dei topi d'oltreoceano. La procedura di rimozione di una palla varia a seconda della marca del topo. La protezione delle palle dei topi d'oltreoceano può essere semplicemente fatta saltare via con un fermacarte, sulla protezione dei topi americani deve essere prima esercitata una rotazione in senso orario o antiorario. Normalmente le palle dei topi non si caricano di elettricità statica, ma è comunque meglio trattarle con cautela, così da evitare scariche impreviste. Una volta completata la sostituzione, il topo può essere utilizzato immediatamente. Si raccomanda al personale esperto di portare costantemente con sé un paio di palle di riserva, così da garantire la massima soddisfazione dei clienti. Nel caso in cui le palle di ricambio scarseggino, è possibile inviarne richiesta alla distribuzione centrale utilizzando i seguenti codici ..."

Numeri e successioni: riflessioni metamatematiche, storiche e didattiche su di un brano leopardiano (4)

4. Dall'aspetto storico a quello didattico
Un'esplicita attenzione alla concezione operativa, dunque, è alla base di alcuni
importanti tentativi di formalizzazione dell'aritmetica. Un tale atteggiamento è
costante nella storia della matematica, come rilevano F. Arzarello, L. Bazzini e
G. Chiappini:
«Lo sviluppo del concetto di numero si può vedere come lo svolgimento di
una catena di passaggi dalle concezioni operative a quelle strutturali. D'altra
parte, anche prima che i processi generatori di nuovi numeri fossero considerati
come oggetti, i matematici li usavano e li combinavano in operazioni» (Arzarello,
Bazzini & Chiappini, 1994, p. 9).

Concludiamo osservando che l'annotazione storica secondo la quale molto
spesso l'aspetto operativo precede quello strutturale, assume una netta rilevanza
in numerose questioni di didattica della matematica (8).
A. Sfard, in una nota ricerca (1991), dopo avere sottolineato la sostanziale
astrazione che caratterizza la matematica (9), sottolinea la possibilità di
concepire (e di presentare) parallelamente i contenuti matematici in termini
strutturali (interpretandoli, dunque, come "oggetti") ed in termini operativi
(interpretandoli, dunque, come "processi"):
«Saper vedere un'entità matematica come un oggetto significa essere capaci
di riferirsi ad essa come ad una cosa reale, una struttura statica... e di manipolarla
come un tutto... Interpretare una nozione come processo significa considerarla
come entità potenziale piuttosto che attuale, che viene alla luce a fronte di
una sequanza di azioni. Quindi, mentre la concezione strutturale è statica..., itananea
e complessiva, quella operativa è dinamica, sequenziale e particolareggiata
» (Sfard, 1991, p. 4).
La Sfard, inoltre, estende tale distinzione alle codifiche (e l'Autrice sembra
qui riprendere idealmente le annotazioni di Leopardi precedentemente citate):
«Le codifiche verbali non possono essere colte 'a colpo d'occhio' e debbono
essere elaborate sequenzialmente, dunque sembrano più adatte per presentare
procedure di calcolo. In tal modo, la rappresentazione interna non iconica è più
pertinente al modo di pensare operativo» (Sfard, 1991, p. 7, con riferimento a:
Hadamard, 1949, p. 77).
Pur senza pretendere di esaurire un argomento assai profondo e delicato, anche
dal punto di vista epistemologico, possiamo dunque concludere che l'introduzione
operativa di molti concetti fondamentali della matematica (e, tra
questi, degli elementi dell'aritmetica) è una questione particolarmente
importante e dibattuta anche in ambito didattico.

Numeri e successioni: riflessioni metamatematiche, storiche e didattiche su di un brano leopardiano (3)

3. L'impostazione intuizionista: i numeri e il conteggio


Faremo quindi riferimento, in questo paragrafo, all'impostazione intuizionista
dell'aritmetica (5) di R.L. Goodstein (1957). Impiegheremo i seguenti simboli:
N operatore di conteggio
a, b, ..., l, ... oggetti
a&b, a&b&c, ..., L, L&a, ... insiemi di oggetti
Definiamo ricorsivamente l'atto del contare (6):
N(l) = 1
N(L&l) = N(l)+1
Sia S l'operatore che porta a considerare il successore (con Sx indicheremo
cioè il successore di x).
L'usuale operazione di addizione:
(a; b) → a+b
è definita ricorsivamente da:
x+0 = x
x+Sy = S(x+y)
Ad esempio, per determinare 6+3 si procede nel modo seguente:
6+0 = 6
6+1 = 7
6+2 = (6+1)+1 = 7+1 = 8
6+3 = (6+2)+1 = 8+1 = 9
La moltiplicazione:
(a; b) → F1(a; b) = a·b
è definita ricorsivamente da:
F1(x; 0) = 0


F1(x; Sy) = x+F1(x; y)
È quindi possibile una definizione ricorsiva di altre operazioni. Per ogni n
naturale, n≥2, definiamo ricorsivamente le operazioni:
Fn(x; 0) = 1
Fn(x; Sy) = Fn–1[x; Fn(x; y)]
Ad esempio, per n = 2 si ottiene la definizione ricorsiva di F2(a; b) = ab
(operazione di esponenziazione) (7):
F2(x; 0) = 1
F2(x; Sy) = F1[x; F2(x; y)] = x·xy
Per n = 3 si ottiene la definizione ricorsiva di un'operazione non usuale, che
possiamo indicare mediante la posizione F3(a; b) = ba:
F3(x; 0) = 1
F3(x; Sy) = F2[x; F2(x; y)] = (yx)x
Risulta ad esempio:
F3(x; 1) = 1x = x
F3(x; 2) = 2x = x^x
F3(x; 1) = 3x = x^x^x

Numeri e successioni: riflessioni metamatematiche, storiche e didattiche su di un brano leopardiano (2)

2. Uno sguardo alla storia:
l'impostazione assiomatica di Peano
Dal punto di vista storico, osserva N. Bourbaki:
«Prima del XIX secolo, pare non vi sia stato alcun tentativo di definire l'addizione
e la moltiplicazione dei numeri naturali se non richiamandosi
direttamente all'intuizione; Leibniz è il solo che, fedele ai propri principi, fa
espressamente notare che delle "verità evidenti" come 2+2 = 4 sono anch'esse
suscettibili di dimostrazione se si riflette sulle definizioni dei numeri che vi
figurano; egli non riteneva affatto come scontata la commutatività
dell'addizione e della moltiplicazione. Ma non spinge oltre le sue riflessioni a
questo proposito, e, verso la metà del XIX secolo, nessun progresso si era
ancora compiuto» (Bourbaki, 1963).
Con il lavoro Sul concetto di numero (1891), Giuseppe Peano (1858-1932),
rielaborando alcune idee introdotte da Wilhelm Richard Dedekind (1831-1916)
nello scritto Was sind und was sollen die Zahlen? (1888), propose un'introduzione
assiomatica dell'aritmetica basata su tre concetti primitivi (l'unità, che in
una seconda stesura fu sostituita con lo zero; il numero; il successivo) e su sei
assiomi (definitivamente enunciati nel 1898 in Aritmetica, la II parte del II vol.
del Formulaire de mathematiques: Peano, 1908, p. 27; Kennedy, 1983):

Assioma zero. I numeri formano una classe (2).
Assioma I. Lo zero è un numero.
Assioma II. Se a è un numero, il suo successivo a+ è un numero.
Assioma III. Se s è una classe contenente lo zero e, per ogni a, se a appartiene
a s, il successivo a+ appartiene a s,; allora ogni numero naturale è in s
("principio di induzione": si tratta in effetti di uno schema di assiomi: Chang &
Keisler, 1973) (3).
Assioma IV. Se a e b sono due numeri e se i loro successivi a+, b+ sono uguali,
allora a e b sono uguali.
Assioma V. Se a è un numero, il suo successivo a+ non è zero.
L'addizione secondo Peano si basa sulle due condizioni seguenti, date nella
simbologia originale (Peano, 1908, p. 29):
Addizione I. Se a è un numero, a+0 = a.
Addizione II. Se a e b sono due numeri, a+(b+) = (a+b)+.
È evidente la stretta analogia che lega l'introduzione di Goodstein
(presentata nel paragrafo precedente) a questa. Per induzione, quindi, Peano
dimostra che se a, b sono numeri, anche a+b è un numero (si veda: Peano,
1908; alcune dimostrazioni sono riportate in: Carruccio, 1972).
La relazione introdotta da Peano è un'applicazione: a→a+ avente per dominio
l'insieme dei numeri naturali e per codominio l'insieme dei numeri naturali
non nulli, e che è una biiezione. Si può inoltre dimostrare che Peano introduce
nell'insieme dei numeri naturali un ordine stretto.

Possiamo dunque concludere che dall'impostazione peaniana, basata sull'applicazione
che ad ogni numero naturale associa il suo successivo, emerge il
ruolo essenziale del concetto di successione.

http://blog.blogosfere.it/mte/mt-tb.php?tb_id=232196

Per i 4 amici che leggono il mio "scatolone di cose", che sono stato recensito come esempio "quello che non deve fare un autore di blog". 
Siccome il mio recensore ha ragione spero di rendergli giusta fama (e di alleggerire la pena), segnalando il suo post che mi condanna: http://sciencebackstage.blogosfere.it/2010/07/le-buone-pratiche-del-blogging.html e aggiungendo SCIENCEBACKSTAGE (http://sciencebackstage.blogosfere.it) al blog rool qui a fianco.

LUCA PACIOLI 500 Anni Dopo

Ed ecco il comunicato stampa:


Il 21 ottobre 2010, con la presentazione degli Atti del Convegno di studi Pacioli 500 anni dopo (Sansepolcro, 22 e 23 maggio 2009), è stato ripercorso l’iter del Progetto Pacioli e sono stati illustrati gli esiti del biennio di studi e ricerca, che ha coinvolto studiosi, docenti e studenti delle scuole medie superiori della Valtiberina toscana e umbra, con la collaborazione degli Enti Locali, e di Soggetti e Imprese operanti nel Territorio. Sono intervenuti i Professori James Banker, Argante Ciocci, Roberto Manescalchi, Enzo Mattesini, Pier Daniele Napolitani, Fausto Casi (Mostra A scuola di scienza e tecnica) e Giovanni Cangi (Quaderno Pacioli fra Arte e Geometria). Ha introdotto la Prof.ssa Paola Refice, Presidente della Fondazione Piero della Francesca. Ha condotto Matteo Martelli, Presidente del Centro Studi Mario Pancrazi.
Nella Sala Conferenze della Fondazione Piero della Francesca, in Viale Aggiunti a Sansepolcro, il folto pubblico ha partecipato alla ricostruzione della figura intellettuale di Luca Pacioli ed ha avuto modo di constatare la validità scientifica del volume degli Atti. Dagli interventi degli studiosi e dei docenti è emerso che il volume del Centro Studi non solo rappresenta un aggiornamento importante delle conoscenze biografiche del frate del Borgo, ma raccoglie gli studi più aggiornati sull’opera del francescano, dà conto del suo contributo all’affermazione della lingua della scienza tra fine Quattrocento e inizi del Cinquecento, illumina i rapporti tra Luca e Piero e tra Luca e Leonardo, nel contesto dell’affermazione delle scienze matematiche, colloca il Pacioli come protagonista della grande rivoluzione della stampa a caratteri mobili.
Il volume sarà presentato, dal Presidente del Centro, il 10 Novembre 2010 a Leòn in Spagna, nel corso dei lavori del VII Encuentro Internacional dell’AECA. Ad un pubblico di esperti di ragioneria e di economia aziendale, sarà illustrato il programma di valorizzazione dell’opera di Pacioli promosso dagli Enti Locali, da Aboca Museum e dal Centro Studi “Mario Pancrazi”. Partendo dal Convegno del 1994 (Luca Pacioli e la Matematica del Rinascimento) sarà illustrata la bibliografia pacioliana fino al volume degli Atti. Un’attenzione particolare sarà rivolta alle pubblicazione delle Edizioni Aboca, dalla monografia pacioliana di Argante Ciocci (2009) all’edizione in facsimile di tre manoscritti del minorita di Sansepolcro: il De ludo scachorum (2007), il De viribus quantitatis (2009), il De divina proportione (manoscritto della Biblioteca Universitaria di Ginevra) del 2010.
Il Centro Studi “Mario Pancrazi” nei prossimi mesi pubblicherà il terzo quaderno della Serie R&D diretta da Francesca Giovagnoli, frutto del seminario dedicato all’astronomia il 31 gennaio 2010 (Sala Conferenze del Museo Diocesano di Città di Castello) e parteciperà alla realizzazione, in collaborazione con Impresa Appennino Centrale – Sindacato di Territorio e il Convitto INPDAP “Regina Elena”, al seminario di economia intitolato Dopo la crisi – Lavoro/Impresa/Società (Sala Teatro Convitto INPDAP, 3 e 4 dicembre 2010). Sono in cantiere, infine, due iniziative: il Progetto Leonardo e la Valtiberina, che prevede un seminario di studi e la pubblicazione degli Atti entro la fine del 2011 e un Incontro Internazionale il 19 Giugno a Sansepolcro che farà il punto sulla biografia pacioliana e sull’importanza del frate matematico nella storia della ragioneria e dell’economia d’azienda.

Numeri e successioni: riflessioni metamatematiche, storiche e didattiche su di un brano leopardiano (1)

di GIORGIO TOMASO BAGNI


1. Zibaldone di pensieri, 28 novembre 1820
Scriveva il ventiduenne Giacomo Leopardi:
«L'uomo senza la cognizione di una favella, non può concepire l'idea di un
numero determinato. Immaginatevi di contare trenta o quaranta pietre,
senz'avere una denominazione da dare a ciascheduna, vale a dire, una, due, tre,
fino all'ultima denominazione, cioè trenta o quaranta, la quale contiene la
somma di tutte le pietre, e desta un'idea che può essere abbracciata tutta in uno
stesso tempo dall'intelletto e dalla memoria, essendo complessiva ma definita
ed intera. Voi nel detto caso, non mi saprete dire, né concepirete in nessun
modo fra voi stesso la quantità precisa delle dette pietre; perché quando siete
arrivato all'ultima, per sapere e concepire detta quantità, bisogna che l'intelletto
concepisca, e la memoria abbia presenti in uno stesso momento tutti
gl'individui di essa quantità, la qual cosa è impossibile all'uomo. Neanche
giova l'aiuto dell'occhio, perché volendo sapere il numero di alcuni oggetti
presenti, e non sapendo contarli, è necessaria la stessa operazione simultanea e
individuale della memoria. E così se tu non sapessi fuorché una sola
denominazione numerica, e contando non potessi dir altro che uno, uno, uno;
per quanta attenzione vi ponessi, affine di raccogliere progressivamente
coll'animo e la memoria, la somma precisa di queste unità, fino all'ultimo; tu
saresti sempre nello stesso caso. Così se non sapessi altro che due
denominazioni ecc. Eccetto una piccolissima quantità, come cinque o sei, che
la memoria e l'intelletto può concepire senza favella, perché arriva ad aver
presenti simultaneamente tutti i pochi individui di essa quantità... In genere
l'idea precisa del numero, o coll'aiuto della favella o senza, non è mai
istantanea, ma composta di successione, più o meno lunga, più o meno
difficile, secondo la misura della quantità» (da Zibaldone di pensieri, 28
novembre 1820: Leopardi, 1969).
Questo brano suggerisce alcune riflessioni sul concetto di numero naturale.

Innanzitutto, appare evidente la centrale importanza che l'Autore attribuisce
al linguaggio (1). Già dall'esordio («L'uomo senza la cognizione di una favella,
non può concepire l'idea di un numero determinato»), infatti, Leopardi si riferisce
esplicitamente al ruolo essenziale della denominazione dei singoli numeri
naturali: è grazie alla «denominazione» che possiamo numerare gli elementi di
un insieme finito (ovvero che possiamo identificare, progressivamente, i suoi
sottoinsiemi di cardinalità crescente) fino a giungere all'indicazione della
totalità (a fissare «un'idea che può essere abbracciata tutta in uno stesso tempo
dall'intelletto e dalla memoria, essendo complessiva ma definita ed intera»).
Questa concezione numerica è dunque strettamente legata al conteggio, all'atto
di enumerare: il ruolo della «favella» viene ad essere decisivo proprio in
quanto consente lo svolgersi della corretta esecuzione pratica di tale atto («E
così se tu non sapessi fuorché una sola denominazione numerica, e contando
non potessi dir altro che uno, uno, uno...»). Leopardi, verso la fine del brano citato,
riconosce chiaramente che il concetto stesso di numero, mediante (ed oltre)
la successione delle «denominazioni», si lega inscindibilmente al
conteggio («L'idea precisa del numero, o coll'aiuto della favella o senza, non è
mai istantanea, ma composta di successione») (Borgato & Pepe, 1998).
Questa considerazione può essere modernamente ripresa ed approfondita
con l'esame di alcune impostazioni dell'aritmetica, che come vedremo basano
le proprie radici sull'introduzione ricorsiva.

The Abraham Lincoln connection

Dal sito http://www.mathopenref.com/euclid.html

At age forty, Abraham Lincoln studied Euclid for training in reasoning, and as a traveling lawyer on horseback, kept a copy of Euclid's Elements in his saddlebag. In his biography of Lincoln, his  law partner Billy Herndon tells how late at night Lincoln would lie on the floor studying Euclid's geometry by lamplight. Lincoln's logical speeches and some of his phrases such as "dedicated to the  proposition" in the Gettysburg address are attributed to his reading of Euclid.

Lincoln explains why he was motivated to read Euclid: "In the course of my law reading I constantly came upon the word "demonstrate". I thought at first that I understood its meaning, but  soon became satisfied that I did not. I said to myself, What do I do when I demonstrate more than when I reason or prove? How does demonstration differ from any other proof?

I consulted Webster's Dictionary. They told of 'certain proof,' 'proof  beyond the possibility of doubt'; but I could form no idea of what sort of proof that was. I thought a great many things were proved beyond the possibility of doubt, without recourse to any such extraordinary process of reasoning as I understood demonstration to be. I consulted all the dictionaries and books of reference I could find, but with no better results. You might as well have defined blue to a blind man.

At last I said,- Lincoln, you never can make a lawyer if you do not understand what demonstrate means; and I left my situation in Springfield, went home to my father's house, and stayed there till I could give any proposition in the six books of Euclid at sight. I then found out what demonstrate means, and went back to my law studies."

Riflessioni sulla matematica greca 3 / Le implicazioni filosofiche del concetto di numero

di Giuseppe Boscarino (http://www.lascuolaitalica.it/vsVII1.htm#N10)

Premessa

“Da tempo immemorabile la filosofia s’è posta la domanda: che cos’è un numero naturale? Tale domanda è oggi viva non meno che nel passato, poiché nessuna delle molte risposte che si è tentato di darle può dirsi pienamente soddisfacente”.¹

È proprio vero!

Fin dall’antichità si sono avute infinite discussioni sull’“essenza” dei numeri.

Anche oggi, con una frequenza che non accenna a decrescere, si scrivono libri su libri che riguardano l’argomento. Ma con una profonda differenza rispetto al passato: in tempi meno recenti si potevano registrare diverse concezioni dei numeri e si scrivevano libri ed articoli di riviste dove i vari autori vi esponevono le proprie idee in aperta polemica tra di loro; quindi, indipendentemente dal giudizio che si voglia dare sulle diverse proposte filosofiche, si può certamente dire che tali autori facevano un lavoro creativo, se non altro, al fine di trovare la loro risposta “pienamente soddisfacente”, cioè in accordo con la propria personale visione del mondo; oggi, invece, sembra che tutti i nuovi scrittori si ritrovino d’accordo nel proclamare che le idee di Dedekind e di Cantor si sono affermate per la ragione che, a parte piccoli dettagli, costoro rappresentano il pensiero più maturo e coerente che, finalmente, ha sistemato le cose, rimaste immutate per millenni dopo Euclide; il quale ultimo, a loro dire, le aveva sì messe in una pregevole forma, ma ancora per qualche verso difettosa; solo con la nuova concezionedell’“assiomatica” si son potuti mettere in chiaro tali difetti.

Poiché tale pretesa chiarezza dell’assiomatica moderna non è mai riuscita a farmi capire, non dico l’“essenza” dei numeri, ma nemmeno a cosa mai potessero servire e, pensando che ciò fosse dovuto al fatto che i vari autori che andavo leggendo non erano sufficientemente esaurienti, anche a ragione della mia formazione prevalentemente filosofica, ho continuato a inseguire questi vari dossografi moderni nei loro difficili discorsi; finché, un bel giorno, mi sono chiesto: ma, se la cosa ormai è così assodata e così chiara, perché mai tutta questa profusione di libri che sembrano dire la stessa cosa? e perché il lettore, alla fine, ne sa meno di prima?

Dopo qualche riflessione mi son convinto che i numeri erano solo il prete sto perché ognuno potesse proclamare la propria metafisica senza, peraltro, dirlo molto chiaramente, in modo da non far scoprire il trucco; scoperta che, ovviamente, avrebbe potuto far crollare tutto il castello di parole “difficili”, mettendo in chiara evidenza, alla fine, la banalità della “cosa in sé”.

Sia Euclide, sia Dedekind sono stati ora elogiati e ora rimproverati per il loro presunto platonismo (naturalmente a seconda dei punti di vista dei vari critici).

Avevo letto che Dedekind ha separato i numeri dalle grandezze e li ha qualificati come libere “creazioni” dell’intelletto umano (ho, in seguito, verificato che tali affer mazioni appartenevano allo stesso Dedekind, che parlava di eine freie Schöpfung).²

Mi son chiesto: ammesso che tale separazione sia possibile, senza aver prima concretamente sperimentato con la realtà fisica, basterebbe tale “creazione” per ricevere la qualifica di platonico? Riandando alle mie antiche letture di Platone e di Aristotele, mi pareva che si dovesse qualificare il Dedekind come anti-platonico, dal momento che Platone, e questo viene confermato dal suo allievo Aristotele, dava i numeri come già esistenti, anche se a mezza strada tra il mondo sensibile e quello iperuraneo, per cui non avrebbero avuto bisogno di alcuna creazione.

Secondo l’interpretazione di Peano, leggendo Euclide (e io penso che lo stesso valga per Pitagora e per Archimede), i numeri ci si presentano come semplici rapporti di grandezze omogenee a una comune grandezza assunta come unità di misura. Se così fosse la filosofia di Euclide rappresenterebbe l’esatto contrario di quella di Platone e anche di quella di Dedekind, per quelle cose che quest’ultimo possa avere in comune con Platone, e tuttavia si legge, anche, che lo stesso Euclide era un platonico.³

Ho concluso che il concetto di numero non è questione che riguardi la scienza, sia pur essa la matematica, ma la metafisica; per cui ho pensato che il problema fosse alla mia portata e così ho cercato di capire, intanto, le polemiche avutesi, nell’antichità, in merito alla questione. Anche perché ho intuito che la sostanza della questione è molto più importante di quanto si possa pensare a prima vista; ciò in quanto tale problematica coinvolge questioni essenziali e di grande rilevanza sociale e politica, e cioè il rapporto tra la matematica e le altre scienze e quindi il rapporto tra queste e la società.

Questo spiegherebbe il fatto che, ancora oggi, si stampano valanghe di libri di vulgativi in cui vengono magnificate le conquiste della scienza moderna, le quali vengono, invariabilmente, attribuite a questo miracoloso cambio di paradigma re gistratosi in seguito alle meno antiche battaglie svoltesi a cavallo tra i due ultimi secoli.

Nelle molte chiacchiere che oggi si ripetono, con uniforme ossessività (tali da stomacare anche il più ben disposto lettore, al sentire che finalmente si è trovata la “verità”), viene asserita la “necessità” di tale “nuova” concezione, la quale è tardata a venire solo a causa della resistenza opposta dai pregiudizi di scienziati filosoficamente ritardatari; e, tra questi, viene spesso annoverato il Peano insieme a tutta la sua scuola.⁴

Per cui, la maggior parte dei filosofi moderni tende a sottovalutare i contributi che tale scuola ha dato, anche a livello puramente filosofico, in relazione ai fonda menti della matematica.

Ma, a ben guardare, si scopre che le cosiddette “nuove frontiere” della mate matica non sono tanto nuove, visto che dagli stessi divulgatori si fanno risalire a Platone e ad Aristotele.

Dopo qualche fatica mi è sembrato di essere riuscito a mettere un po’ d’ordine nelle mie idee e ho sentito la necessità di parteciparle ad altri, cogliendo l’occasione di una decisione, già da molto tempo presa, di andare pubblicando sui Quaderni di Mondotre alcuni significativi brani, tratti dalle opere di Peano, che oggi non sono più facilmenti reperibili per lo studioso non specialista, il quale volesse rimeditare au tonomamente su tali questioni, che oggi, invece, vengono date come definitivamente risolte dalla miracolosa scienza del Novecento.

Pitagora e Platone

(ovvero del numero ideale e del numero matematico).

La prima cosa che val la pena chiarire è il rapporto tra Platone e la tradizione pitagorica.

Su tale problema le opinioni sono molto discordi, stante la difficile interpreta zione delle fonti. Come è stato riportato nella nota³, dalle opere di Platone ben poco se ne può cavare; e poiché Proclo è massimamente inaffidabile, non ci resta che rivolgerci al giudizio del discepolo stesso di Platone e, cioè, Aristotele:

“La dottrina di Platone, la quale per molti aspetti si ricollega alle dottrine pitagoriche, possiede anche una propria originalità, che la separa dalla filosofia degli Italici ...” (Metafisica 987a, 30-32);

“Platone ha introdotto, come cosa nuova, soltanto il termine partecipazione, giacché mentre i Pitagorici asseriscono che le cose esistono per imitazione dei numeri, egli dice che esistono per partecipazione, limitandosi a cambiare solo il nome. Ma di qual natura fosse mai l’imitazione o partecipazione delle forme ideali, è una questione che essi hanno lasciata insoluta. Platone aggiunge ancora che, oltre gli oggetti e le forme ideali, esistono, come qualcosa di intermedio, le entità matematiche, le quali differiscono dalle cose sensibili, perché sono eterne ed immobili, e differiscono dalle forme ideali perché c’è una pluralità di enti matematici che si somigliano, mentre ogni forma ideale è di per sé unica, individuale e singolare ...” (Metafisica 987b, 10-19);

..... egli [Platone] afferma che i numeri esistono al di fuori degli oggetti sensibili, mentre i Pitagorici sostengono che gli stessi oggetti sono numeri, e non pongono gli enti matematici come qualcosa di intermedio tra forme e oggetti sensibili. La concezione della trascendenza dell’uno e dei numeri rispetto alle cose — concezione diversa da quella dei Pitagorici — e l’introduzione della dottrina delle idee furono il risultato delle sue ricerche di carattere logico ...”(Metafisica 987b, 28-32).

Da questi brani aristotelici sembra emergere che, secondo lo Staginita, Platone si distacca dalla concezione pitagorica dei numeri, almeno in un punto; e cioè nel concepire una diversa relazione tra i numeri e le cose sensibili.

Anche se, polemicamente, Aristotele fa finta di sottovalutare le differenze tra le due concezioni che (secondo le sue parole) si ridurrebbe ad un semplice cambiamento di nome, quando non si definisca esattamente il significato di imitazione e partecipa zione, tuttavia nota che, alla divisione aristotelica tra oggetti e forme ideali, Platone vi sistema nel mezzo le entità matematiche.

Certo per Aristotele era assurdo, come in altri passi delle sue opere afferma, identificare i numeri con le cose come, ingenuamente a suo giudizio, facevano i pita gorici, ma ben più assurda era la pretesa platonica di triplicare le cose; ad Aristotele bastava il semplice sdoppiamento.

Le tre concezioni, qui delineate, hanno un’enorme rilevanza in merito al rapporto tra scienza e mondo reale.

Nella filosofia degli Italici, dalla quale Platone si distacca, il mondo sensibile è mera apparenza, semplicemente Caos, la vera realtà coincide con la nostra ricostru zione razionale, effettuata con procedimenti puramente logici e matematici. Quindi i numeri, in quanto rapporti tra grandezze, sono la “realtà” stessa. Oltre tali rapporti non c’è e non ci può essere nient’altro che non siano le informi e mutevoli sensazioni, sulle quali niente si può dire se non cantare le oscure odi eraclitee.

Platone assegna loro tre distinti gradi di realtà, gerarchicamente sistemati: in alto il mondo delle idee, ineffabile; in basso il mondo sensibile, volgare; nel mezzo la matematica che però non serve per capire il mondo sensibile che, d’altronde, non merita tale attenzione, ma solo per sollecitare il ricordo del mondo iperuraneo della perfezione assoluta.

Per Aristotele, invece, la vera realtà coincide con il mondo dei sensi, i nomi delle cose, li inventiamo noi per classificare le nostre esperienze e, anche se li usiamo in molti sensi, essi ne hanno uno proprio che si identifica con 1’“essenza” della cosa.

“Ora, tra gli oggetti di cui si dà la definizione — ossia tra le essenze — ce ne sono alcuni che si presentano nello stesso modo del camuso, altri nello stesso modo del concavo. E la differenza tra questi due gruppi di cose sta nel fatto che il camuso viene concepito insieme con la materia (giacché il camuso è un naso curvo), mentre il concavo prescinde dalla materia sensibile. Se, allora, tutti i termini fisici sono usati in un’accezione simile a quella di camuso — ad esempio, naso, occhio, viso, carne, osso e, in genere, animale, oppure foglia, radice, corteccia e, in genere, pianta (e in realtà ciascuna di queste cose non può essere definita ove si prescinda dal movimento, e quindi possiede sempre una materia) —, risulta allora evidente il modo in cui si deve ricercare l’essenza e formulare la definizione nell’ambito delle cose naturali e per quale motivo rientri nel compito del fisico estendere l’indagine anche su certi aspetti dell’anima che non siano concepibili come indipendenti dalla materia.” (Metafisica 1025b, 31-37; 1026a, 1-7).

Sarebbe inutile chiedere ad Aristotele cos’è mai tale essenza. Se ne uscirebbe con altre parole il cui significato riuscirebbe ancora più oscuro; ma, in ogni caso, egli rifiuta ogni intermediario tra parole e cose e non vede alcuna necessità di creare un mondo a parte per le entità matematiche. Esse di per sé stesse sono forme ideali perfette e, in quanto tali, non possono applicarsi alle cose terrene (“...gli enti matematici, tranne quelli che hanno a che fare con l’astronomia, sono privi di movimento” — Metafisica 989b, 31). Ma su questo punto si ritrova d’accordo con Platone.

Ma è proprio questo punto che segna il distacco profondo tra i pitagorici, da un lato, che sostengono l’unità di essere e di pensiero e, dall’altro lato, la molteplicità dei mondi (trina o bina che sia) di Platone e di Aristotele.

Ed è su questa fondamentale discriminante che, nel corso dei secoli, si e mani festata la battaglia sulla concezione della scienza.

Naturalmente sarebbe importante capire il significato che Platone e Aristotele attribuiscono al termine “esistenza” (risultando, invece, chiaro il significato che gli attribuiscono gli Italici, come sottolinea lo stesso Aristotele).⁵

Ma questo ci condurrebbe a una lunga maratona, data la “vaghezza” con cui tali autori adoperano il termine, in tutte le loro opere; e non solo in riferimento al “numero” ma, soprattutto, in riferimento alla cosiddetta “teoria delle idee” o delle “forme ideali”. Per cui ci conviene lasciar correre!

Aristotele nella molto ambigua, e perciò misteriosa, frase: “c’è una pluralità…” sembra voler dire che per Platone i numeri preesistano all’atto stesso del pensare, anche se non allo stesso modo delle idee, data la pluralità che ha ogni numero in contrasto con la singolarità dell’idea.

Notiamo, a questo punto, che per Dedekind invece i numeri cominciano ad esistere proprio e solo in virtù dell’atto stesso del pensare, per cui dobbiamo ancora trovare il punto di congiunzione tra Platone e Dedekind e, soprattutto, tra Platone ed Euclide; dal momento che, dalla lettura dei suoi “Elementi”, quest’ultimo non sembra avere una concezione diversa da quella che Aristotele, attribuisce ai Pitagorici; per non menzionare il fatto che Peano, come si vedrà dai brani qui riportati in appendice, elucidando la teoria delle grandezze di Euclide, ne mostra una grande ammirazione e, nello stesso tempo, mostra che, per quanto c’è di vero, quella di Dedekind è indistinguibile da quella di Euclide; mentre, in altre occasioni, mostra di avere una non troppo alta stima di Platone, quantomeno per quanto riguarda la matematica, come abbiamo visto nella citazione che abbiamo riportato in nota³.

Ma vediamo quali erano gli intendimenti di Dedekind:

“considero il concetto di numero del tutto indipendente dalle rappresentazioni o intuizioni dello spazio e del tempo, e lo ritengo piuttosto una emanazione diretta delle leggi del pensiero”

E nel suo più famoso lavoro⁶ scrive:

“Finora di norma per introdurre i numeri irrazionali ci si richiamava diretta mente al concetto di grandezza estensiva — che però a sua volta non è mai stato rigorosamente definito — e si definivano quei numeri come il risultato della misura zione di una grandezza per mezzo di un’altra grandezza omogenea. Io invece credo che l’aritmetica si sviluppi da se stessa”.

Ecco il principale obbiettivo di Dedekind: svincolarsi dalle grandezze e, quindi, dalla fisica!

Personalmente, non ho mai capito questo imperioso desiderio dei matematici e dei logici a svincolarsi dalla fisica e di volere definire nominalmente ogni cosa. Il tentativo dei logici medioevali ha prodotto le interminabili discussioni sul sesso degli angeli.

Ma la storia è molto più antica!

Testimonia Porfirio:⁷

“Inoltre i Pitagorici dicono che Platone e Aristotele, Speusippo, Aristosseno, Senocrate, si appropriarono di tutto ciò ch’era fruttuoso nella dottrina e con poca fatica, mentre invece raccolsero insieme e aggiudicarono alla scuola pitagorica, come suo proprio, tutto quello ch’era superficiale e vano o tutto quello ch’era stato affer mato da maligni calunniatori per dileggiare la scuola stessa”.

Per sapere a quale scopo fecero questo, forse, è utile leggere questa satira di Ateneo:⁸

“A. Che dire di Platone, e di Speusippo e Menedemo? a che attendono ora? quali cure, quale discorso è oggetto del loro investigare? Questo saggiamente, se qualcosa ne sai, dimmi, per la terra ... — B. So chiaramente che dire di loro: vidi infatti alle Panatee la schiera di quei giovani nei ginnasi dell’Accademia tenervi discorsi indicibili, assurdi. Dando definizioni sulla natura, separando la natura degli animali e quella delle piante e le specie dei vegetali. Poi fra questi la zucca presero in esame, di che genere sia. — A. E che definizione diedero del genere a cui appartiene la pianta? Spiegamelo, se lo sai. — B. Dapprima tutti, muti, stettero intenti e curvi e rifletterono per lungo tempo. Poi d’improvviso, mentre ancora erano curvi e investigavano i giovani, uno di loro disse che è un vegetale rotondo, uno ch’è verdura, un altro ch’è albero. Ascoltando ciò un medico venuto dalla Sicilia si rivoltò contro dicendo che deliravano. — A. Si adirarono allora per la derisione e gridarono? Far così in una riunione è sconveniente. — B. Non se la presero molto i giovani. Platone poi, ch’era presente, molto dolcemente e senza adirarsi, fece loro di nuovo la zucca dall’inizio esaminare per definirne il genere: ed essi procedettero alla divisione.”

Infatti, anche oggi, dopo la “grande svolta epistemologica” anche la matema tica è diventata tassonomia; non si contano più gli “spazi”, sono innumerevoli le “geometrie” e di “assiomatiche” ne abbiamo a bizzeffe!

Il problema delle definizioni era oggetto di interminabili discussioni tra i discepoli di Platone; alcuni, come Speusippo, interpretando malamente le affermazioni dei Pi tagorici, negavano in principio la possibilità stessa di poter definire alcunché, perché per definire qualcosa bisognava prima conoscere tutte le cose del mondo; altri, come Aristotele, sosteneva che ciò era invece possibile per successive dicotomizzazioni.

Sentiamo, in proposito, l’opinione dell’aristotelico Eustrato:⁹

“Ma poiché Speusippo sembra aver voluto sostenere con un ragionamento credibile il principio per cui tentava di distruggere dalle radici la scienza della definizione e dimostrava come sia impossibile definire alcunché, occorre non trascurare il suo discorso senza esaminano, come se fosse uno scherzo gettato là a intralcio del pro cedere della scienza, ma rimuoverlo dal nostro cammino, con confutazioni basate sulla verità. Lo scopo del definire, egli dice, consiste nello stabilire l’essenza speci fica dell’oggetto definito; e questo non potrebbe avvenire in altro modo se non col distinguerlo per mezzo del ragionamento da tutte le altre cose. Non potrebbe però fare queste distinzioni chi non conoscesse tutte le differenze nella loro singolarità. E non potrebbe conoscere tutte le differenze nella loro singolarità chi non conoscesse tutte le realtà individue. Perciò chi definisce qualcosa deve, in pari tempo, conoscere tutte le realtà individue. Ma è chiaro che deve necessariamente sapere le differenze dei singoli oggetti colui che voglia distinguerli gli uni dagli altri mediante definizione. Se non vi è differenza delle realtà individue fra di loro, non vi è alcuna differenza reciproca (è per la differenza che il differente è tale); se poi non vi è differenza re ciproca, ne consegue che le realtà individue sono uguali l’una all’altra. Invece esse sono altre reciprocamente, e quindi la differenza esiste. Se esiste si deve poterla co noscere: altrimenti non si saprà come le cose differiscano le une dalle altre, né alcuno potrà formulare un ragionamento che separi il medesimo dagli altri. E perciò, per poter definire qualcosa, bisogna conoscere tutte le cose. Questo è il ragionamento di Speusippo, mediante il quale sembra ch’egli negasse la stessa possibilità di definire”.

Dopo questa lunga disamina dei ragionamenti di Speusippo, Eustrato conclude rifacendosi all’autorità di Aristotele, il quale dice:

“…non occorre affatto che chi definisce e opera le divisioni conosca tutti gli oggetti reali. Senonché, affermano alcuni, è impossibile conoscere le differenze tra un oggetto e ciascuno degli altri oggetti, senza conoscere ciascuno di questi altri oggetti; ma non è neppure possibile conoscere tali oggetti, se non se ne conoscono le differenze rispetto all’oggetto in questione: due oggetti sono infatti identici, quando tra di essi non sussiste una differenza, e sono diversi, quando tale differenza sussiste. Ora, ciò anzitutto è falso, poiché due oggetti non risultano diversi in virtù di una qualsiasi differenza.” (Anal. Post., 97a, 7).

Come risolve Dedekind questo problema?

Già Kronecker gli aveva aperto la strada dichiarando che i numeri interi li aveva creati Dio e tutto il resto era stato creato dall’uomo; per cui, visto che c’era la possibilità di tali creazioni, Dedekind ha creato i numeri reali asserendone l’esistenza per “assioma” (ma, come si legge in Appendice, Peano nega che possa essere un assioma e, d’altra parte, non può essere una definizione; sembra che la sola possibilità che rimaneva a Dedekind era la “creazione dal nulla”, a immagine e somiglianza di Dio); ma Cantor lo ha superato “creando” i numeri transfiniti, d’allora in poi, le “creazioni” non si contano più.

Ma vediamo cli capire gli assunti metafisici che stanno alla base delle varie po sizioni che, come abbiamo visto, sono vecchie quanto il mondo.

Per far questo ci serviremo dell’ideografia di Peano.

Con il termine “differenze” (διαφοράί) deve intendersi “proprietà, classe, nome comune…”, con il termine “realtà individue” (‘έχαστον) deve intendersi “individui”.

La relazione tra individuo e proprietà è ideografata con x Î a, dove x è l’individuo, a la proprietà, Î (è un) è la relazione esistente tra i due concetti.

Dato un gruppo di proprietà si può generare tutto un “reticolo” di proprietà,¹⁰ ordinate dalla relazione di inclusione É . Gli “atomi” del reticolo (cioè le proprietà che si riferiscono a un singolo individuo) sono da Peano chiamati “elementi” e in dicati con ι x . Usando la terminologia di Leibniz, il ragionamento di Speusippo si può rendere nel seguente modo: Non si può costruire una proprietà mediante la sua “estensione”, cioè a partire dagli “individui” x, in quanto questi sono cono sciuti solo quando ne conosciamo gli “elementi” ι x, cioè per“intensione”; ma per conoscere gli “elementi” occorrerà conoscere tutte le proprietà del reticolo, che sole le possono rendere, per “intersezione logica”; ma, per conoscere tutte le proprietà, per l’ipotesi che abbiamo fatto che esse sono conosciute solo mediante gli individui, dobbiamo conoscere tutti gli individui e così abbiamo chiuso un circolo vizioso. Se ne deve concludere che gli individui non sono definibili e, si potrebbe aggiungere, devono esistere autonomamente nel mondo iperuraneo delle idee. Fiat individuum et individuum fuit.

Aristotele si limita a dire che tale ragionamento è erroneo dichiarando la falsità dell’assunto, in quanto gli sembra evidente il contrario; ma, come sempre, non offre alcuna spiegazione alternativa, anche perché non riesce a vedere la differenza tra “individuo” ed “elemento” e continua a frullare dei termini scarsamente definiti come: “principio, sostanza, essenza, sostrato, causa, idea, forma, ecc.. Infatti:

“Ci sono, però, alcuni che, come i Pitagorici e Speusippo, ritengono che il bello e il bene, nel loro sommo grado, non risiedano nel principio, perché a loro avviso, i principi delle piante e degli animali sono cause, mentre la bellezza e la perfezione risiedono soltanto in ciò che dai principi viene prodotto. Ma siffatte credenze sono errate. In realtà, il seme proviene da altri esseri anteriori che sono già perfetti, e la prima cosa non è affatto il seme, ma ciò che è già perfetto; così, ad esempio, si può dire che anteriore al seme è l’uomo, non, però, quello che proviene dal seme, bensì un altro da cui il seme stesso proviene.” (Metafisica 1072b, 30 e sg.).

Sistematicamente Aristotele, quando parla dei Pitagorici, si riferisce al ritratto che di loro fanno i Platonici, che si dicono i loro veri continuatori, e li contesta con una miscela esplosiva di empirismo estremo e di estremo razionalismo. Intuisce che oltre l’uomo prodotto dal seme c’è qualche cosa d’altro, ma non riconoscendo che quest’altro è il “concetto di uomo”, o proprietà di essere uomo che dir si voglia, fa derivare dal concetto di uomo il concetto di seme, come dire che il nome del seme deriva dal nome dell’uomo.

La filosofia dei Pitagorici, invece, è sommamente dialettica (nel senso moderno del termine): non esistono le idee nel mondo iperuraneo, non esistono le cose nel mondo delle sensazioni, le idee sono, semplicemente, la nostra ricostruzione razionale (= logica = matematica) del mondo, il quale ci bombarda con innumerevoli sensa zioni informi. Senza le sensazioni non possono esistere le idee (= cose), senza le idee (= cose) non potrebbero esistere i numeri, il mondo e le cose non sono separati, le cose sono i numeri stessi.

Ecco, dopo le conseguenze disastrose delle diatribe tra platonici ed aristotelici, che hanno portato alle elaborate teorie sul sesso degli angeli, sono arrivati i vari Keplero, Galilei, Cavalieri, Newton, ecc., che sono ritornati agli antichi, attraverso il grande Archimede.

Ma, come si sa, il bello dura poco; e così sono venuti fuori i vari Dedekind, Cantor, Hilbert, ecc. che ritornano a Platone e ad Aristotele, senza però ricono scerlo; come, invece, fecero i primi con l’esternare la loro profonda riconoscenza ad Archimede.

La ricostruzione ideografica di molti libri degli Elementi di Euclide, fatta dal Peano, si ispira a questa più antica, e più autenticamente scientifica, filosofia:

“la determinazione dei postulati fondamentali, si può fare seguendo la solita via. Si scrivano tutte le proprietà che risultano dall’osservazione del moto fisico. Si scindano queste proposizioni in tante affermazioni semplici; e poi si esamini quali di queste affermazioni sono già implicitamente contenute nelle rimanenti. Procedendo avanti in questo esame, finché sarà pòssibile, troveremo un gruppo di affermazioni esprimenti verità irriduttibili tra loro, e che costituiscono i postulati del moto.” (Opere Scelte, vol. III, p. 142).

Ecco risolto ogni problema di definizione, di assiomatizzazione e di dimostra zione.

Separando tra loro matematica e fisica, logica e filosofia, si può solo parlare del sesso degli angeli.

Ma leggiamo ora direttamente il commento di Peano all’opera di Dedekind con siderata in relazione all’opera di Euclide.

E curioso notare che nel Formulario Mathematico, dove Peano e collaboratori con incredibile pignoleria registrano accanto ad ogni formula l’autore che ne viene accredidato come il primo scopritore, non compare invece assolutamente il nome di Dedekind, mentre si dà credito a Cantor della definizione di potenza (= cardinalità); ma la ragione di ciò emerge chiaramente dai passi riportati in Appendice.

Ma, per concludere questa mia breve introduzione, cercherò di rispondere alla mia domanda iniziale. E’ Dedekind un platonico? Lo è Euclide?

Se per “platonico” si intende colui che pensa che abbia o possa avere “esistenza ontologica” qualcosa oltre il sensibile allora Dedekind è certamente un platonico, ma Euclide non lo è perché quest’ultimo si limitava all’asserzione di una “esistenza logica” come chiarita da Parmenide e come in tutta la tradizione Italica, come rico nosciuto dallo stesso Aristotele.

Se si restringe l’estensione dell’aggettivo, escludendo gli atti di creazione da parte degli uomini, allora Dedekind non lo è; e nemmeno sarebbe classificabile nel novero dei mistici, in quanto questi usano riservare le creazioni solo a Dio.

NOTE

1.       Tratto da T. Viola, Introduzione alla teoria degli insiemi, Boringhieri, 1965, p. 124 TORNA

2.       “Noi siamo di stirpe divina e certamente abbiamo facoltà di creare non soltanto cose materiali (ferrovie, telegrafi), ma  tipicamente cose mentali” da una lettera di Dedekind a Weber, in J.W.R. Dedekind, Scritti sui fondamenti della matematica, a cura di F. Gana, Bibliopolis, 1982). TORNA

3.       “Non è qio il caso di esporre ampiamente una veduta che a nostro avviso è difficilmente confutabile: l’affermazione che il pensiero filosofico che è stato presente a Euclide nella coposizione dei suoi Elementi è quello di Platone soprattutto. La tradizione, d’altra parte, dipinge Euclide come un platonico…” tratto da A. Frajese, Attraverso la storia della matematica, Le Monnier, 1977, p. 106. A leggere questo libro uno riceve l’impressione che la matematica sia una creazione di Platone, restavano solo i numeri da creare e ci ha pensato Dedekind! Ma c’è stato qualcuno che ha avuto l’ardire di mettere in dubbio questa “veduta difficilmente confutabile”: “Alcuni autori attribuiscono a Platone degli studi sugli irrazionali (Baltzer, Elem. D. Mathem. A. 1885 p. 100; Encyclop. p. 49). Invero nei dialoghi di questo filosofo trovansi qua e là dei termini matematici, ma riuniti in modo così incerto da farli ritenere come parole difficili con cui un interlocutore cerca confondere l’avversario; all’incirca come nei giornali politici del giorno d’oggi sta scritto incommensurabile invece di grandissimo. Il passo più volte citato, nella Πολιτεία  VIII  546 è considerato dai commentatori Jowett and Campbell, Oxford a. 1894, come un riddle. Al più da un passo del Θεαίτήτος 143 E, si può dedurre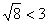, e ciò parmi la cosa più importante contenuta in quelle opere su questo soggetto.”, G.Peano, Opere Scelte, vol. III, Ed. Cremonese, Roma, 1958, p. 249. Ma come si è permesso Peano di scrivere tali cose! Con quale autorità!  TORNA

4.       Si leggano gli incredibili giudizi tranciati da C. Mangione nella Storia del pensiero…di Geymonat, sui quali ho già avuto modo di commentare sul n. 4-5 dei Quaderni di Mondotre. TORNA

5.       “…i cosiddetti Pitagorici si dedicarono per primi alle scienze matematiche, facendole progredire; e poiché trovarono in esse il loro nutrimento, furono del parere che i principi di queste si identificassero con i principi di tutte le cose…credevano di scorgere in quelli, più che nel fuoco o nella terra o nell’acqua, un gran numero di somiglianze con le cose che esistono…e, insomma, pareva loro evidente che tutte le altre cose modellassero sui numeri la lro intera natura e che i numeri fossero l’essenza primordiale di tutto l’universo fisico;” (Metafisica 985b, 23 – 35); “A certuni sembra che i limiti del corpo – ossia la superficie, la linea, il punto e la monade – siano sostanze, e lo siano persino in modo più autentico che non il corpo o il solido.” (Metafisica 1028b, 16 – 18). TORNA

6.       Stetigkeit und irrazionale Zahhlen (vedi a pag. 68 del citato libro a cura di Gana); la citazione precedente si trova a p. 79-80.  TORNA

7.       Porph. Vita Pythag. 53, p. 46, riportato in Speusippo – Frammenti, a cura di M. Isnardi Parente, Bibliopolis, 1980, p. 145.  TORNA

8.       Athen. Deipnosoph. II 59 d-f, riportato in Speusippo …, p. 145.  TORNA

9.       Eustrat. Arist. Anal. Post., p. 202. Riportato in Speusippo …, p. 151.  TORNA

10.   Vedi l’articolo sui Presocratici di Notarrigo nel numero 4-5 dei Quaderni di Mondotre.  TORNA