Matematica addio?

Copio&incollo da Roberto Natalini sul blog Culture dell'Unità:
http://www.unita.it/culture/matematica-addio-e-berlusconi-br-fa-un-errore-marchiano-1.329853



La scuola sta per ricominciare. In questi ultimi giorni di vacanze, quando al mare c'è poca gente e i bagnini sono già impegnati a riporre sdraio e ombrelloni per la prossima stagione, ho visto bambini e ragazzi di tutte le età, ai tavoli del mio stabilimento balneare, intenti a compitare con occhi spiritati, pagine e pagine di esercizi di matematica apparentemente di una noia mortale (ho evitato di indagare troppo, bastavano gli occhi spiritati). Alcuni di loro in realtà non hanno mai smesso durante l'estate. Questi ragazzi si stanno unendo ad un esercito in marcia, l'esercito di coloro che odiano la matematica.
Che ci sia un problema lo sappiamo tutti. Nonostante gli sforzi eroici di alcuni (molti) insegnanti validi e preparati, la quasi totalità degli studenti rimane con un'impressione profondamente sbagliata. Dopo 13 anni di studio (5 di elementari+ 3 di medie + 5 di superiori), la maggior parte delle persone, non solo in breve tempo avrà grosse difficoltà a fare un ragionamento matematico che vada al di là delle quattro operazioni (fate un test con un trentenne medio su cosa si ricordi della matematica studiata a scuola), ma soprattutto avrà sviluppato un'incredibile avversione verso questa scienza, che solo nel migliore dei casi si declinerà in un semplice riconoscimento di inadeguatezza ("proprio non la capivo") con annesso senso di colpa, quando non si sarà trasformata in un vero e duraturo disgusto (e odio verso i professori di matematica). È vero, questo succede un po' per tutte le materie. I capolavori della letteratura italiana e straniera, una volta passati per il "tritacarne scolastico", difficilmente conserveranno il loro fascino (incidentalmente, è forse una fortuna che parti essenziali della cultura contemporanea, come il cinema, i fumetti, la musica (non classica), la letteratura contemporanea, non vengano toccati in modo sostanziale dal suddetto tritacarne). Ma per la matematica questo problema è sicuramente più marcato.
Ha ragione Paul Lockart nel suo "A mathematician's lament" (tradotto in Italia con il titolo forse un po' disorientante "Contro l'ora di matematica") quando dice che il metodo usato per l'insegnamento della matematica oggi, corrisponderebbe per la musica a imparare tutta la notazione musicale e le regole dell'armonia senza mai arrivare a suonare una nota. Manca insomma la cosa principale, imparare ad affrontare problemi interessanti, e ci si concentra molto sulla nomenclatura (ascissa e ordinata, numeratore e denominatore, quoto (sic! mi sono dovuto far spiegare cosa fosse), apotema, minuendo e sottraendo, equazioni numeriche fratte), e su regole abbastanza inutili. Le regole sulle proporzioni che confondono solo le idee e poi, dopo un anno di esercizi, non si trova un adulto che capisca le percentuali(*). L'inutile regola di Ruffini. Le formule di prostaferesi, senza mai far vedere cose interessanti come il calcolo della distanza di oggetti reali con la trigonometria. La razionalizzazione, che forse nasce nei tempi in cui i numeri irrazionali non erano ben capiti e accettati, ma che non ha senso in nessun contesto moderno (ma perché non dovrei dividere per radice di 2?). Una matematica arbitraria, mnemonica che spegne le idee e si presenta con la spigolosità, e anche il fascino, di un contratto assicurativo dove siamo sempre noi ad avere le peggio (e un sacco di roba è scritta piccola piccola). Non ci si abitua ad avere delle idee, a impostare i problemi, a capire le connessioni tra le cose e mancano del tutto l'immaginazione e la fantasia,  che invece sono ciò che meglio caratterizza la matematica.
Cosa si può fare allora concretamente per cambiare le cose? Di idee ce ne sono tante in giro, e il sito divulgativo Maddmaths! della Società Italiana di Matematica Applicata e Industriale, ha appena aperto un Forum per cercare di raccogliere idee per rendere più attraente l'insegnamento della matematica. Io intanto mi sono letto il bellissimo libro Matematica e Realtà di Emma Castelnuovo e Mario Barra (del 1976, ristampato nel 2000). Contiene i materiali del laboratorio svolto dal gruppo della Castelnuovo presso la scuola media (sic!) Tasso di Roma nel 1974. Ci sono rettangoli di area massima (ma anche solidi di volume massimo), il bellissimo Teorema di Pick (lo conoscete?), variazioni esotiche sul teorema di Pitagora (tipo le lunule di Ippocrate), Fibonacci, le spirali, le serie convergenti e divergenti, alcune proprietà bellissime della cicloide, definita come "la curva percorsa dalla vavola della nostra bicicletta" (per esempio si dimostra che l'area sotto la cicloide è 3 volte l'area del cerchio che la genera, cosa che Galileo ai suoi tempi non riuscì a calcolare), la topologia con la Formula di Eulero, i grafi e il problema dei ponti di Königsberg. Scrive la Castelnuovo, a proposito della Cicloide, subito dopo averne riportato la definizione presa da un testo universitario: "La definizione è concisa e rigorosa, ma nello stesso tempo arida e priva di ogni suggestione. Suona quasi comeuna frettolosa necrologia della cicloide stessa, e, tacendo sulle notizie storiche, le applicazioni e le proprietà di cui gode, viene presentata come un argomento di studio cervellotico, senza motivazioni. In particolare, si prescinde dalla considerazione che, per studiare bene qualsiasi cosa è necessario, se non proprio l'amore per l'argomento, almeno l'apprezzamento, la simpatia o il riconoscimento di un'utilità concreta. Inoltre spesso, avendo a disposizione degli strumenti molto potenti, si tende a limitare il piacere del ragionamento particolare e a soffocare l'intuizione e il saper vedere la matematica." 
Potrebbe essere questo l'insegnamento più importante da tenere presente. Insomma servirebbe, da parte degli insegnanti in primo luogo, più che nuovi strumenti didattici o tecnologie o altre diavolerie (tipo Internet, che è una cosa bellissima, ma sembra diventata la soluzione a tutto quello che non vogliamo dover affrontare veramente), la riscoperta del senso del divertimento nel fare matematica. Bisognerebbe risvegliare le energie nascoste dei ragazzi, che di solito, quando vedono qualche formula entrano nel panico e bloccano qualsiasi processo mentale. Come dice il grande matematico Terence Tao (medaglia Fields 2006) in un bell'articolo tradotto dal suo blog, tra le qualità che un matematico deve sviluppare c'è sicuramente la capacità di fare domande stupide. Oggi questo non è incoraggiato nella scuola, e forse è da lì che bisogna ricominciare. Togliere la matematica dal piedistallo e portarla a spasso in cortile, tra l'altalena e i giochi con la palla. Che se fosse un disegno, non sarebbe la copia di quadri di autori famosi, ma disegni di bambini pieni di libertà, magari solo scarabocchi colorati. Che se fosse una musica, sarebbe imparare a trovare la propria, anche cominciando solo dal fare un rumore sgradevole per vedere l'effetto che fa, seguire un ritmo stupido che poi a un certo punto si fa interessante. Una matematica in cui si possa provare a dividere per zero e capire come questo comporti dei problemi (in fondo è da lì che sono partite le derivate, no?). Dove non ci siano "trucchi" o "regole", ma ragionamenti e intuizioni. Una matematica che porti a "vedere" e "capire" e non solo a "calcolare". Una matematica forse un po' meno formale e un po' più sostanziale. Il tempo per lavorare duro ci sarà sempre. Come per tutte le cose difficili, c'è un tempo per creare motivazione ed entusiasmo, e uno per un lavoro profondo e sistematico di assorbimento, per la costruzione di vere e proprie nuove connessioni cerebrali. Nessuno farebbe estenuanti allenamenti sportivi, o sessioni intensive di danza, se non fosse profondamente motivato a farlo. Ma se c'è la motivazione, non per forza uno straordinario talento innato, il resto viene molto (più) facile...



(*) Come dimostra la storia del nostro Presidente del Consiglio, che in alcune intercettazioni pubblicate recentemente ha detto di fidarsi di Letta "non al cento per cento, ma al cento per mille". Se sapesse le proporzioni, saprebbe che questo vuol dire fidarsi di Letta al 10%. Se fossi Letta non sarei contento...

Pappo di Alessandria e le Collezioni Matematiche

Da un po' di tempo rifletto sulle connessioni esistenti fra le matematiche antiche e quelle moderne e quanto siano importanti per queste ultime, le conoscenze ereditate da quelle più antiche. In questo quadro di pensieri, un nome viene spesso alla mante di chi ha letto qualcosa di storia delle matematiche. Pappo d'Alessandria. Chi è costui, si chiederanno tutti quelli che l matematica l'hanno studiata a scuola. Il nome dice poco ma in realtà il suo lavoro è stato un formidabile resoconto della matematica ellenistica e soprattutto la riscoperta delle sue carte è stato un vero "boost" per la rinascita delle scienze e delle matematiche nel Rinascimento.  Per tentare di onorare la memoria di Pappo, ripropongo una bella paginetta tratta dal sito web del Prof. Montanari dell'Università degli Studi di Ferrara: http://web.unife.it/altro/tesi/A.Montanari/Pappo.htm

Dalla morte di Apollonio, la geometria classica non aveva più trovato nessun sostenitore. Tuttavia, durante il regno di Diocleziano (284-305), visse ad Alessandria uno scienziato animato dallo spirito che aveva posseduto Euclide, Archimede e Apollonio: Pappo di Alessandria. Verso il 320 compose un'opera dal titolo Collezioni matematiche, di cui possiamo vedere la prima pagina nella traduzione fatta da Commandino e pubblicata nel 1588 a Pesaro.

Quest'opera è molto importante in quanto ci fornisce una preziosa documentazione storica concernente alcuni aspetti della matematica greca che altrimenti sarebbero rimasti sconosciuti. Per esempio, è dal Libro V delle Collezioni che siamo venuti a sapere della scoperta di Archimede dei tredici poliedri semiregolari, noti come "solidi archimedei" (è possibile trovare una traduzione in inglese del passo del Libro V [47]). Le Collezioni contengono anche dimostrazioni alternative e lemmi supplementari relativi a teoremi di Euclide, Archimede, Apollonio e Tolomeo. Infine, il trattato presenta nuove scoperte e generalizzazioni che non è dato trovare in nessuna opera precedente.
Essa è suddivisa in 8 libri di cui il primo è andato completamente perduto e il secondo perduto in parte. In questo caso, la perdita è meno grave di quella degli ultimi libri dell'Arithmetica di Diofanto: sembra infatti che i primi due libri riguardassero prevalentemente i principi del sistema di tetradi introdotto da Apollonio nella numerazione greca.
Nel Libro III Pappo fa una netta distinzione tra problemi "piani", "solidi" e "lineari": i primi sono costruibili solo con cerchi e rette, i secondi sono risolvibili mediante l'uso di sezioni coniche e l'ultimo genere di problemi richiede curve diverse da rette, cerchi e coniche. Pappo descrive poi alcune soluzioni dei tre famosi problemi dell'antichità: la duplicazione del cubo e la trisezione dell'angolo vengono presentate come problemi del secondo tipo, ossia come problemi solidi, e la quadratura del cerchio come un problema lineare. In questo contesto Pappo afferma virtualmente che i problemi classici presentano soluzione impossibile sotto le condizioni platoniche, poiché non appartengono alla categoria dei problemi piani. Tuttavia, solo nel XIX secolo si giunse a dare dimostrazioni rigorose di tale fatto.
Nel Libro IV Pappo torna a insistere sul fatto che ogni problema richiede una costruzione appropriata. In altre parole, non si dovrebbero usare luoghi geometrici lineari nella soluzione di un problema solido, né luoghi geometrici solidi o lineari nella soluzione di un problema piano. Considerando la trisezione di un angolo come un problema solido, suggerisce pertanto metodi che fanno uso di sezioni coniche, mentre Archimede in un caso aveva usato una neusis ossia una costruzione del tipo di quella su cui è basato il regolo calcolatore e in un altro caso era ricorso alla spirale, che è un luogo geometrico lineare.
Nel Libro IV troviamo anche delle generalizzazioni di teoremi precedenti. Per esempio vi è la generalizzazione del teorema di Pitagora: se ABC è un triangolo qualsiasi e se ABDE e CBGF sono parallelogrammi qualsiasi costruiti su due dei lati, allora Pappo costruisce sul lato AC un terzo parallelogramma ACKL uguale alla somma degli altri due. Per esaminare il metodo utilizzato si può accedere al sito L'area di Pappo [48]. Un altro esempio di generalizzazione è costituito da un'estensione dei teoremi di Archimede sul "coltello del calzolaio". Tale generalizzazione afferma che, se si inscrivono successivamente cerchi P¹, P², P³, ... come nella Fig. 1, tutti tangenti ai semicerchi costruiti su AB e su AC, e successivamente tangenti l'un l'altro, la distanza perpendicolare misurata dal centro dell'n-esimo cerchio alla base ABC è uguale a n volte il diametro dell'n-esimo cerchio.

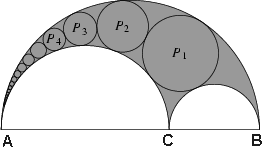Fig. 1

Il V libro contiene la trattazione dei problemi di isoperimetria, compresa la dimostrazione che il cerchio possiede, per un dato perimetro, un'area maggiore di qualsiasi poligono regolare. Altri risultati sono:

1. tra i poligoni regolari, a parità di perimetro, quello che ha area più grande è quello che ha il maggior numero di lati;

2. tra tutti i triangoli di assegnato perimetro, con la stessa base, quello che ha area maggiore è l’equilatero;

3. tra i poligoni, quelli con area maggiore sono le figure convesse, in particolare i poligoni regolari.

Qui sembra che Pappo abbia seguito il trattato Sulle figure isometriche scritto quasi mezzo millennio prima da Zenodoro (180 a.C. circa), di cui sono stati conservati dei frammenti di altri commentatori posteriori. Fra i teoremi del trattato di Zenodoro vi era quello che afferma che tra tutte le figure solide con uguale superficie la sfera possiede il massimo volume, ma ne veniva data solo una giustificazione incompleta.
I Libri VI e VIII riguardano principalmente le applicazioni della matematica all'astronomia, all'ottica e alla meccanica (compreso un tentativo di trovare la legge del piano inclinato).
Il Libro VII riveste un ruolo primario per la storia della matematica, nel campo della geometria analitica.
La geometria greca si era limitata, fino a quel momento, allo studio di curve piane; è pertanto significativo il fatto che Pappo presenti in questo libro un problema generalizzato che comporta un numero infinito di nuove curve. Questo problema è noto come il "problema di Pappo"; la sua formulazione originaria, però, che comporta tre o quattro rette, sembra risalire al tempo di Euclide e sembra che si debba una sua soluzione ad Apollonio. Nondimeno da Pappo si ricava l'impressione che i matematici precedenti non siano riusciti a darne una soluzione generale; egli conferma, così, implicitamente di essere stato il primo a mostrare che tale soluzione è in tutti i casi una sezione conica. Inoltre, Pappo considerava il problema analogo per più di quattro rette. Nel caso di sei rette giacenti in un piano, egli riconosceva che una curva è determinata dalla condizione che il prodotto delle distanze da tre delle rette abbia un rapporto fisso con il prodotto delle distanze delle altre tre. Pappo esitava a considerare casi che comportassero più di sei rette per la ragione che

non esiste nessuna cosa che sia contenuta da più di tre dimensioni.

Pappo non approfondì oltre lo studio di questi luoghi geometrici, ma fu senz'altro questo problema, ripreso in seguito da Descartes, il punto di partenza per l'elaborazione della geometria analitica.
In questo libro vi è poi un'esposizione completa del metodo analitico e viene descritta una raccolta di opere precedenti che hanno utilizzato il metodo di analisi e di sintesi, nota come il Tesoro dell'analisi. Pappo descrive l'analisi come

un metodo consistente nel considerare come ammesso ciò che si cerca e nello sviluppare le conseguenze sino a giungere a qualcosa che viene ammesso come risultato nella sintesi.

Quindi, egli considerava l'analisi come una "soluzione alla rovescia", i cui passi andavano ripercorsi in senso inverso perché potesse costituire una dimostrazione valida. Se l'analisi porta a qualcosa che si ammette essere impossibile, anche il problema sarà impossibile, poiché una falsa conclusione implica una falsa premessa.
Tra le opere costituenti il Tesoro dell'analisi Pappo elenca i trattati sulle coniche di Aristeo, di Euclide e di Apollonio. Circa la metà delle opere elencate da Pappo sono andate perdute, tra cui la Sezione di un rapporto di Apollonio e i trattati Sulle medie di Eratostene e Sui porismi di Euclide.
Nel Libro VII compaiono teoremi molto importanti, tra i quali quello noto come "teorema di Pappo" sugli esagoni [49]:

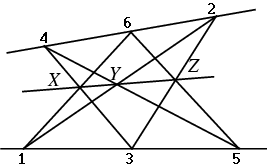Dato un esagono di vertici 1, 2, 3, 4, 5, 6, se i vertici di indice dispari appartengono a una retta e quelli d'indice pari a un'altra retta complanare, allora i punti X, Y, Z di incontro di coppie di lati opposti dell'esagono sono allineati.

Una generalizzazione del teorema di Pappo è il teorema di Pascal [50] su un esagono inscritto in una conica, e nel sito Configurazione di Pappo per i cerchi [51] si possono studiare in movimento i casi in cui le rette sono sostituite da iperboli e ellissi.
Un altro teorema che compare qui per la prima volta è quello che solitamente viene indicato col nome di Paolo Guldino, un matematico del XVII secolo (vedi teorema di Pappo-Guldino [52]):

Se una curva piana chiusa viene fatta ruotare intorno a una retta che non attraversa la curva, il volume del solido così generato viene calcolato facendo il prodotto dell'area delimitata dalla curva per la distanza percorsa durante la rotazione dal centro di gravità dell'area.

Pappo era orgoglioso di questo teorema estremamente generalizzato: esso comprendeva infatti "un gran numero di teoremi di ogni sorta concernenti curve, superfici e solidi, i quali venivano dimostrati tutti simultaneamente mediante un'unica dimostrazione". Tale teorema è il più generale che si conosca nell'antichità relativamente al campo dell'analisi infinitesimale.


Le Collezioni matematiche di Pappo è l'ultimo trattato matematico veramente significativo dell'antichità, poiché il tentativo da lui fatto di ridare alla geometria nuova vitalità non fu coronato dal successo. Si continuarono a scrivere opere matematiche in greco per un altro millennio circa, ma gli autori che vennero dopo Pappo non raggiunsero mai il suo livello. Le loro opere hanno quasi esclusivamente la forma di commento a trattati anteriori. Lo stesso Pappo è parzialmente responsabile del proliferare di commenti del genere: anch'egli aveva composto commenti agli Elementi di Euclide e all'Almagesto di Tolomeo, ma di questi sono pervenuti solo dei frammenti. Commenti posteriori, come quelli di Teone di Alessandria, sono più utili per le informazioni storiche che contengono che non per i risultati matematici presentati.